
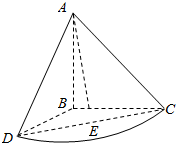
 等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:
等腰直角三角形ABC中,AB=BC=2,将斜边AC绕直角边AB旋转90°后得到旋转体A-BCD,如图所示,求:分析 (1)连结BE,则∠AEB为直线AE与面BCD所成的角.
(2)由BD⊥BC,BD⊥AB可推出BD⊥平面ABC,故BD⊥AC.
(3)分别求出两个几何体的体积.
解答 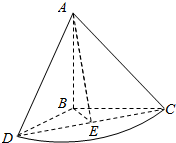 解:(1)连结BE,∵AB⊥BC,AB⊥BD,BC∩BD=B,BC?平面BCD,BD?平面BCD,
解:(1)连结BE,∵AB⊥BC,AB⊥BD,BC∩BD=B,BC?平面BCD,BD?平面BCD,
∴AB⊥平面BCD,∴∠AEB为直线AE与面BCD所成的角.
∵∠DBC=90°,∴CD=$\sqrt{2}$BC=2$\sqrt{2}$,∴BE=$\frac{1}{2}CD$=$\sqrt{2}$.∴tan∠AEB=$\frac{AB}{BE}$=$\sqrt{2}$.∴∠AEB=arctan$\sqrt{2}$.
(2)∵BD⊥BC,BD⊥AB,BC∩AB=B,BC?平面ABC,AB?平面ABC,
∴BD⊥平面ABC,∵AC?平面ABC,
∴BD⊥AC.∴异面直线AC和BD所成的角为90°.
(3)V1=$\frac{1}{3}$S扇形BCD•AB=$\frac{1}{3}×\frac{1}{4}×π×{2}^{2}×2$=$\frac{2π}{3}$.V2=$\frac{1}{3}$S△BCD•AB=$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$.
∴$\frac{{V}_{1}}{{V}_{2}}$=$\frac{π}{2}$.
点评 本题考查了线面垂直的判定与性质,线面角,体积计算,正确找到线面角解题关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(5,7] | B. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(5,7] | C. | ($\frac{1}{5}$,$\frac{1}{3}$]∪(3,5] | D. | ($\frac{1}{7}$,$\frac{1}{5}$]∪(3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x>y | B. | x=y | ||
| C. | x<y | D. | 大小不确定,与m、n的取值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
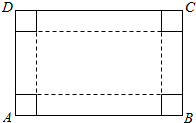 如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).
如图,ABCD是长方形硬纸片,AB=80cm,AD=50cm,在硬纸片的四角切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸箱,设切去的小正方形的白边长为x(cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com