
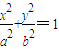 ЃЈaЃОbЃО0ЃЉЃЌЦфНЙОрЮЊ2cЃЌШє
ЃЈaЃОbЃО0ЃЉЃЌЦфНЙОрЮЊ2cЃЌШє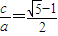 ЃЈЁж0.618ЃЉЃЌдђГЦЭждВCЮЊЁАЛЦН№ЭждВЁБЃЎ
ЃЈЁж0.618ЃЉЃЌдђГЦЭждВCЮЊЁАЛЦН№ЭждВЁБЃЎ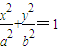 ЃЈaЃОbЃО0ЃЉжаЃЌaЁЂbЁЂcГЩЕШБШЪ§СаЃЎ
ЃЈaЃОbЃО0ЃЉжаЃЌaЁЂbЁЂcГЩЕШБШЪ§СаЃЎ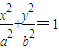 ЃЈaЃОbЃО0ЃЉЕФгвНЙЕуЮЊF2ЃЈcЃЌ0ЃЉЃЌPЮЊЭждВCЩЯЕФШЮвтвЛЕуЃЎЪЧЗёДцдкЙ§ЕуF2ЁЂPЕФжБЯпlЃЌЪЙlгыyжсЕФНЛЕуRТњзу
ЃЈaЃОbЃО0ЃЉЕФгвНЙЕуЮЊF2ЃЈcЃЌ0ЃЉЃЌPЮЊЭждВCЩЯЕФШЮвтвЛЕуЃЎЪЧЗёДцдкЙ§ЕуF2ЁЂPЕФжБЯпlЃЌЪЙlгыyжсЕФНЛЕуRТњзу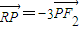 ЃПШєДцдкЃЌЧѓжБЯпlЕФаБТЪkЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃПШєДцдкЃЌЧѓжБЯпlЕФаБТЪkЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ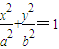 ЃЈaЃОbЃО0ЃЉЕФзѓЁЂгвНЙЕуЗжБ№ЪЧF1ЃЈ-cЃЌ0ЃЉЁЂF2ЃЈcЃЌ0ЃЉЃЌвдAЃЈ-aЃЌ0ЃЉЁЂBЃЈaЃЌ0ЃЉЁЂDЃЈ0ЃЌ-bЃЉЁЂEЃЈ0ЃЌbЃЉЮЊЖЅЕуЕФСтаЮADBEЕФФкЧадВЙ§НЙЕуF1ЁЂF2ЃЎЪдаДГіЁАЛЦН№ЫЋЧњЯпЁБЕФЖЈвхЃЛЖдгкЩЯЪіУќЬтЃЌдкЛЦН№ЫЋЧњЯпжааДГіЯрЙиЕФецУќЬтЃЌВЂМгвджЄУїЃЎ
ЃЈaЃОbЃО0ЃЉЕФзѓЁЂгвНЙЕуЗжБ№ЪЧF1ЃЈ-cЃЌ0ЃЉЁЂF2ЃЈcЃЌ0ЃЉЃЌвдAЃЈ-aЃЌ0ЃЉЁЂBЃЈaЃЌ0ЃЉЁЂDЃЈ0ЃЌ-bЃЉЁЂEЃЈ0ЃЌbЃЉЮЊЖЅЕуЕФСтаЮADBEЕФФкЧадВЙ§НЙЕуF1ЁЂF2ЃЎЪдаДГіЁАЛЦН№ЫЋЧњЯпЁБЕФЖЈвхЃЛЖдгкЩЯЪіУќЬтЃЌдкЛЦН№ЫЋЧњЯпжааДГіЯрЙиЕФецУќЬтЃЌВЂМгвджЄУїЃЎ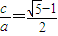 МАb2=a2-c2ЃЌЧѓЕУbгыacЕФЙиЯЕЃЌИљОнЕШБШжаЯюЕФаджЪПЩЭЦЖЯaЁЂbЁЂcГЩЕШБШЪ§СаЃЎ
МАb2=a2-c2ЃЌЧѓЕУbгыacЕФЙиЯЕЃЌИљОнЕШБШжаЯюЕФаджЪПЩЭЦЖЯaЁЂbЁЂcГЩЕШБШЪ§СаЃЎ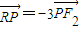 ЃЌНјЖјБэЪОГіPЕФзјБъЃЌАбPЕуДњШыЭждВЕФЗНГЬећРэКѓПЩНтЕУkДцдкЃЌЧѓГіkЃЎ
ЃЌНјЖјБэЪОГіPЕФзјБъЃЌАбPЕуДњШыЭждВЕФЗНГЬећРэКѓПЩНтЕУkДцдкЃЌЧѓГіkЃЎ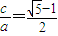 МАb2=a2-c2ЃЌЕУ
МАb2=a2-c2ЃЌЕУ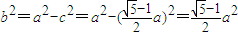 =acЃЌ
=acЃЌ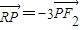 ЃЌ
ЃЌ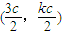 ЃЌ
ЃЌ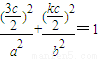 ЃЌ
ЃЌ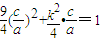 ЃЌ
ЃЌ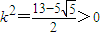 ЃЌ
ЃЌ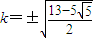 ЃЎ
ЃЎ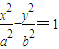 ЕФзѓЁЂгвНЙЕуЗжБ№ЪЧF1ЃЈ-cЃЌ0ЃЉЁЂF2ЃЈcЃЌ0ЃЉЃЌвдF1ЃЈ-cЃЌ0ЃЉЁЂF2ЃЈcЃЌ0ЃЉЁЂDЃЈ0ЃЌ-bЃЉЁЂEЃЈ0ЃЌbЃЉЮЊЖЅЕуЕФСтаЮF1DF2EЕФФкЧадВЙ§ЖЅЕуAЃЈ-aЃЌ0ЃЉЁЂBЃЈaЃЌ0ЃЉЃЎ
ЕФзѓЁЂгвНЙЕуЗжБ№ЪЧF1ЃЈ-cЃЌ0ЃЉЁЂF2ЃЈcЃЌ0ЃЉЃЌвдF1ЃЈ-cЃЌ0ЃЉЁЂF2ЃЈcЃЌ0ЃЉЁЂDЃЈ0ЃЌ-bЃЉЁЂEЃЈ0ЃЌbЃЉЮЊЖЅЕуЕФСтаЮF1DF2EЕФФкЧадВЙ§ЖЅЕуAЃЈ-aЃЌ0ЃЉЁЂBЃЈaЃЌ0ЃЉЃЎ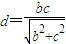 ЃЌ
ЃЌ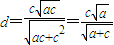 ЃЌгжНЋ
ЃЌгжНЋ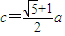 ДњШыЃЌ
ДњШыЃЌ

 аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ
аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ гІгУЬтзївЕБОЯЕСаД№АИ
гІгУЬтзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2010-2011бЇФъИЃНЈЪЁСњбвЪаИпШ§ЃЈЩЯЃЉЦкФЉжЪСПМьВщвЛМЖДяБъЪ§бЇЪдОэЃЈЮФПЦЃЉЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
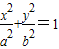 ЃЈaЃОbЃО0ЃЉЕФзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЃЈ-1ЃЌ0ЃЉЁЂF2ЃЈ1ЃЌ0ЃЉЃЌРыаФТЪЮЊ
ЃЈaЃОbЃО0ЃЉЕФзѓЁЂгвНЙЕуЗжБ№ЮЊF1ЃЈ-1ЃЌ0ЃЉЁЂF2ЃЈ1ЃЌ0ЃЉЃЌРыаФТЪЮЊ ЃЎ
ЃЎ ЃЈOЮЊзјБъдЕуЃЉЃЌЧѓЁїAOBЕФУцЛ§ЃЛ
ЃЈOЮЊзјБъдЕуЃЉЃЌЧѓЁїAOBЕФУцЛ§ЃЛВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2013ФъШЋЙњЦеЭЈИпЕШбЇаЃеаЩњЭГвЛПМЪдРэПЦЪ§бЇЃЈЫФДЈОэНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ЃЈ13ЗжЃЉвбжЊЭждВCЃК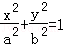 ЃЈaЃОbЃО0ЃЉЕФСНИіНЙЕуЗжБ№ЮЊF1ЃЈЉ1ЃЌ0ЃЉЃЌF2ЃЈ1ЃЌ0ЃЉЃЌЧвЭждВCОЙ§Еу
ЃЈaЃОbЃО0ЃЉЕФСНИіНЙЕуЗжБ№ЮЊF1ЃЈЉ1ЃЌ0ЃЉЃЌF2ЃЈ1ЃЌ0ЃЉЃЌЧвЭждВCОЙ§Еу ЃЎ
ЃЎ
ЃЈIЃЉЧѓЭждВCЕФРыаФТЪЃК
ЃЈIIЃЉЩшЙ§ЕуAЃЈ0ЃЌ2ЃЉЕФжБЯпlгыЭждВCНЛгкMЃЌNСНЕуЃЌЕуQЪЧЯпЖЮMNЩЯЕФЕуЃЌЧв ЃЌЧѓЕуQЕФЙьМЃЗНГЬЃЎ
ЃЌЧѓЕуQЕФЙьМЃЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2014НьИЪЫрЮфЭўСљжаИпЖў12дТбЇЖЮМьВтЮФПЦЪ§бЇЪдЬтЃЈНтЮіАцЃЉ ЬтаЭЃКНтД№Ьт
ЃЈ12ЗжЃЉвбжЊЭждВCЃК ЃЈaЃОbЃО0ЃЉЕФвЛИіЖЅЕуЮЊAЃЈ2,0ЃЉЃЌРыаФТЪЮЊ
ЃЈaЃОbЃО0ЃЉЕФвЛИіЖЅЕуЮЊAЃЈ2,0ЃЉЃЌРыаФТЪЮЊ ЃЌжБЯпy=kЃЈx-1ЃЉгыЭждВCНЛгкВЛЭЌЕФСНЕуMЁЂN.
ЃЌжБЯпy=kЃЈx-1ЃЉгыЭждВCНЛгкВЛЭЌЕФСНЕуMЁЂN.
ЂйЧѓЭждВCЕФЗНГЬ.
ЂкЕБЈSAMNЕФУцЛ§ЮЊ ЪБЃЌЧѓkЕФжЕ.
ЪБЃЌЧѓkЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2011-2012бЇФъНЮїЪЁИпШ§ЕкЦпДЮдТПМРэПЦЪ§бЇ ЬтаЭЃКНтД№Ьт
вбжЊЭждВCЃК +
+ =1(aЃОbЃО0)ЃЌжБЯпy=x+
=1(aЃОbЃО0)ЃЌжБЯпy=x+ гывддЕуЮЊдВаФЃЌвдЭждВCЕФЖЬАыжсГЄЮЊАыОЖЕФдВЯрЧаЃЌF1ЃЌF2ЮЊЦфзѓЁЂгвНЙЕуЃЌPЮЊЭждВCЩЯШЮвЛЕуЃЌЁїF1PF2ЕФжиаФЮЊGЃЌФкаФЮЊIЃЌЧвIGЁЮF1F2ЁЃЂХЧѓЭждВCЕФЗНГЬЁЃЂЦШєжБЯпLЃКy=kx+m(kЁй0)гыЭждВCНЛгкВЛЭЌСНЕуAЃЌBЧвЯпЖЮABЕФДЙжБЦНЗжЯпЙ§ЖЈЕуC(
гывддЕуЮЊдВаФЃЌвдЭждВCЕФЖЬАыжсГЄЮЊАыОЖЕФдВЯрЧаЃЌF1ЃЌF2ЮЊЦфзѓЁЂгвНЙЕуЃЌPЮЊЭждВCЩЯШЮвЛЕуЃЌЁїF1PF2ЕФжиаФЮЊGЃЌФкаФЮЊIЃЌЧвIGЁЮF1F2ЁЃЂХЧѓЭждВCЕФЗНГЬЁЃЂЦШєжБЯпLЃКy=kx+m(kЁй0)гыЭждВCНЛгкВЛЭЌСНЕуAЃЌBЧвЯпЖЮABЕФДЙжБЦНЗжЯпЙ§ЖЈЕуC( ЃЌ0)ЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЁЃ
ЃЌ0)ЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК2010-2011бЇФъеуНЪЁИпШ§ЩЯбЇЦкЕкШ§ДЮдТПМЪ§бЇЮФОэ ЬтаЭЃКбЁдёЬт
вбжЊЭждВCЃК ЃЈa>b>0ЃЉЕФРыаФТЪЮЊ
ЃЈa>b>0ЃЉЕФРыаФТЪЮЊ ЃЌЙ§гвНЙЕуFЧваБТЪЮЊkЃЈk>0ЃЉЕФжБЯпгыЭждВCЯрНЛгкAЁЂBСНЕуЃЌШє
ЃЌЙ§гвНЙЕуFЧваБТЪЮЊkЃЈk>0ЃЉЕФжБЯпгыЭждВCЯрНЛгкAЁЂBСНЕуЃЌШє ЁЃдђ
ЁЃдђ ЃЈ ЃЉ
ЃЈ ЃЉ
ЃЈAЃЉ1 ЃЈBЃЉ2 ЃЈCЃЉ ЃЈDЃЉ
ЃЈDЃЉ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com