
【题目】设函数f(x)=1﹣ ![]() (x∈R),
(x∈R),
(1)求反函数f﹣1(x);
(2)解不等式f﹣1(x)>log2(1+x)+1.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的普通方程;
的普通方程;
(2)已知点![]() 是曲线
是曲线![]() 上一点,求点
上一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() ,曲线
,曲线![]() .以极点为坐标原点,极轴为
.以极点为坐标原点,极轴为![]() 轴正半轴建立平面直角坐标系
轴正半轴建立平面直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为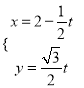 (
(![]() 为参数).
为参数).
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 与
与![]() 交于不同的四点,这四点在
交于不同的四点,这四点在![]() 上排列顺次为
上排列顺次为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an},{bn}满足a1=3,a2=6,{bn}是等差数列,且对任意正整数n,都有 ![]() 成等比数列.
成等比数列.
(1)求数列{bn}的通项公式;
(2)设 ![]() ,试比较2Sn与
,试比较2Sn与 ![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式kx2﹣2x+3k<0.
(1)若不等式的解集为{x|x<﹣3或x>﹣1},求k的值;
(2)若不等式的解集为,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com