解:(1)设x∈[-e,0),则-x∈(0,e]
∴f(-x)=-ax+ln(-x)
由f(x)为奇函数可得,f(-x)=-f(x)
∴-f(x)=-ax+ln(-x)
∴f(x)=ax-ln(-x)
∴
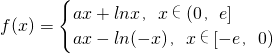
(2)假设存在负数a满足条件
由(1)可得,x∈[-e,0)f(x)=ax-ln(-x)
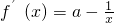
令f′(x)>0可得

,f′(x)<0可得
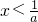
若
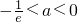
,则函数在
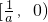
单调递增,在
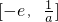
单调递减,则
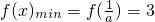
∴
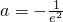
若
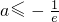
,则函数在[-e,0)单调递增,则
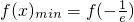
=
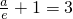
a=2e(舍)
故
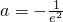
(3)a=-1,f(x)=
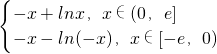
∴|f(x)|=|x|-ln|x|为偶函数,故只要考虑x∈(0,e]时,f(x)=x-lnx>0
而此时,g(x)=
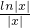
=

,x∈(0,e]
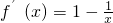
≥0可得,x≥1,f′(x)<0可得,x<1
∴函数f(x)在(0,1]上单调递减,在[1,e]单调递增,则f(x)
min=f(1)=1
∴
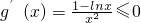
在(0,e]上恒成立,则可得函数g(x)在(0,e]单调递增,则

而
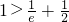
即
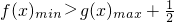
x∈[-e,0)同理可证
∴
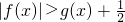
分析:(1)设x∈[-e,0),则-x∈(0,e],从而可得f(-x)=-ax+ln(-x),结合f(x)为奇函数可求f(x),x∈[-e,0)
(2)假设存在负数a满足条件,由(1)可得,x∈[-e,0)f(x)=ax-ln(-x),结合函数的导数
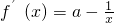
需分,
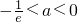
;
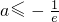
,两种情况判断函数在[-e,0}上的单调性,进而可求函数的最小值,进而可求a
(3)a=-1,f(x)=
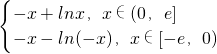
,从而可得|f(x)|=|x|-ln|x|为偶函数,故只要考虑x∈(0,e]时,f(x)=x-lnx>0而此时,g(x)=
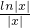
=

,x∈(0,e]
结合
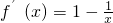
判断函数f(x)的单调性可求f(x)
min=f(1)=1,而
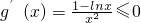
可得

可证
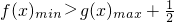
,从而可证
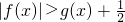
点评:本题主要考查了利用函数的奇偶性求解函数的解析式,及利用函数的导数判断函数的单调性,求解函数的最值,利用单调性证明不等式,解题的关键是熟练应用函数的性质.是综合性较强的试题.

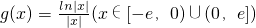 ,求证:当a=-1时,
,求证:当a=-1时,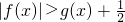 .
.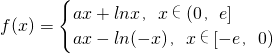
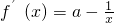
 ,f′(x)<0可得
,f′(x)<0可得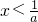
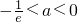 ,则函数在
,则函数在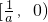 单调递增,在
单调递增,在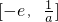 单调递减,则
单调递减,则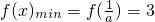
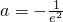
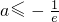 ,则函数在[-e,0)单调递增,则
,则函数在[-e,0)单调递增,则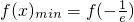 =
=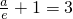
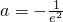
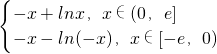
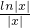 =
= ,x∈(0,e]
,x∈(0,e]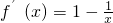 ≥0可得,x≥1,f′(x)<0可得,x<1
≥0可得,x≥1,f′(x)<0可得,x<1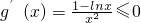 在(0,e]上恒成立,则可得函数g(x)在(0,e]单调递增,则
在(0,e]上恒成立,则可得函数g(x)在(0,e]单调递增,则
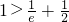 即
即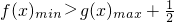
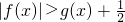
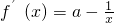 需分,
需分,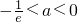 ;
;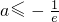 ,两种情况判断函数在[-e,0}上的单调性,进而可求函数的最小值,进而可求a
,两种情况判断函数在[-e,0}上的单调性,进而可求函数的最小值,进而可求a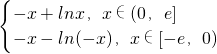 ,从而可得|f(x)|=|x|-ln|x|为偶函数,故只要考虑x∈(0,e]时,f(x)=x-lnx>0而此时,g(x)=
,从而可得|f(x)|=|x|-ln|x|为偶函数,故只要考虑x∈(0,e]时,f(x)=x-lnx>0而此时,g(x)=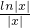 =
= ,x∈(0,e]
,x∈(0,e]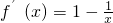 判断函数f(x)的单调性可求f(x)min=f(1)=1,而
判断函数f(x)的单调性可求f(x)min=f(1)=1,而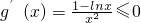 可得
可得 可证
可证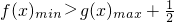 ,从而可证
,从而可证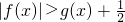


 已知函数f(x)=x+
已知函数f(x)=x+