
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
⑴分别求出函数f(x)和g(x)的解析式;
⑵如果函数y=g(f(x))在区间[1,m)上单调递减,求m的取值范围.

解:⑴由题图1得,二次函数f(x)的顶点坐标为(1,2),
故可设函数f(x)=a(x-1)2+2,
又函数f(x)的图象过点(0,0),
故a=-2,整理得f(x)=-2x2+4x. (3分)
由题图2得,函数g(x)=loga(x+b)的图象过点(0,0)和(1,1),
故有![]() ∴
∴![]()
∴g(x)=log2(x+1)(x>-1). (6分)
⑵由⑴得y=g(f(x))=log2(-2x2+4x+1)是由y=log2t和t=-2x2+4x+1复合而成的函数,而y=log2t在定义域上单调递增,要使函数y=g(f(x))在区间[1,m)上单调递减,必须t=-2x2+4x+1在区间[1,m)上单调递减,且有t>0恒成立 (9分)
由t=0得x=![]() ,又t的图象的对称轴为x=1.
,又t的图象的对称轴为x=1.
所以满足条件的m的取值范围为1<m<![]() . (12分)
. (12分)


科目:高中数学 来源: 题型:
 (2011•南通模拟)
(2011•南通模拟)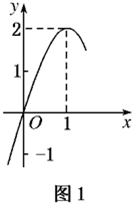 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省荆门市高二(下)期末数学试卷(文科)(解析版) 题型:解答题

 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省新坝中学高三(上)第一次学情调研数学试卷(文科)(解析版) 题型:解答题

 如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.
如图所示:图1是定义在R上的二次函数f(x)的部分图象,图2是函数g(x)=loga(x+b)的部分图象.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省邵阳市洞口四中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com