
【题目】已知函数![]() ,记
,记![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.
(1)当![]() 时,求证:函数
时,求证:函数![]() 的图像(除切点外)均为切线
的图像(除切点外)均为切线![]() 的下方;
的下方;
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)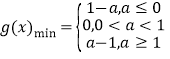
【解析】
(1)求得f(x)的导数,考虑极值点以及函数的凹凸性,即可得证;
(2)讨论a<0,a=0,a>1,a=1,0<a<1时,函数h(x)=f(x)﹣2lnx的导数和单调性,最值,即可得到所求g(x)的最小值.
(1)设切线方程为![]()
记![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() ,即
,即![]() ,当且仅当
,当且仅当![]() 时取“
时取“![]() ”.
”.
故命题成立
(2)![]() .
.
设![]() ,
,![]() ,
,
1)当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,且
上单调递减,且![]() .
.
∴![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
∴![]()
2)当![]() 时,
时,![]() ,
,
设![]() ,
,![]() ,
,![]() 有两根
有两根![]() ,
,![]() ,
,
![]() ,
,![]() ,不妨令
,不妨令![]() ,
,
![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
①当![]() ,即
,即![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,∴
,∴![]() ;
;![]()
②当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
![]() ,
,
存在![]() 使得
使得![]() ,
,
∴![]() .
.
综上可得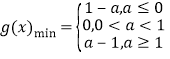 .
.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
【题目】体育测试成绩分为四个等级:优、良、中、不及格.某班50名学生参加测试结果如下:
等级 | 优(86~100分) | 良(75~85分) | 中(60~74分) | 不及格(1~59分) |
人数 | 5 | 21 | 22 | 2 |
(1)估计该班学生体育测试的平均成绩;
(2)从该班任意抽取1名学生,求这名学生的测试成绩为“优”或“良”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系,随机调查100名高一学生,得到![]() 列联表如下:由此得出的正确结论是( )
列联表如下:由此得出的正确结论是( )
选择物理 | 不选择物理 | 总计 | |
男 | 35 | 20 | 55 |
女 | 15 | 30 | 45 |
总计 | 50 | 50 | 100 |
附: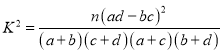
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
A.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别有关”
B.在犯错误的概率不超过0.01的前提下,认为“选择物理与性别无关”
C.有![]() 的把握认为“选择物理与性别有关”
的把握认为“选择物理与性别有关”
D.有![]() 的把握认为“选择物理与性别无关”
的把握认为“选择物理与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元,为了增加企业竞争力,决定优化产业结构,调整出x(x∈N*)名员工从事第三产业,调整后他们平均每人每年创造利润为10(a﹣0.8x%)万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.4x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创遣的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
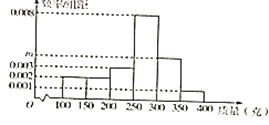
【题目】炎炎夏季,水蜜桃成为备受大家欢迎的一种水果,某果园的水蜜桃质量分布如图所示.
(Ⅰ)求m的值;
(Ⅱ)以频率估计概率,若从该果园中随机采摘5个水蜜桃,记质量在300克以上(含300克)的个数为X,求X的分布列及数学期望;
(Ⅲ)经市场调查,该种水蜜桃在过去50天的销售量(单位:千克)和价格(单位:元/千克)均为销售时间t(天)的函数,且销售量近似地满足f(t)=﹣3t+300(1≤t≤50,t∈N),前30天价格为g(t)=![]() +20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
+20(1≤t≤30,t∈N),后20天价格为g(t)=30(31≤t≤50,t∈N),求日销售额S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com