
分析 (1)由已知条件利用等比数列的性质推导出a3=4,a5=1,从而求出$q=\frac{1}{2},{a}_{1}=16$,由此能求出数列{bn}的通项公式.
(2)由$\frac{1}{{b}_{n}{b}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,利用裂项求和法能求出数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Sn.
解答 解:(1)∵在正项等比数列{an}中,公比q∈(0,1),且a1a5+2a3a5+a2a8=25,
∴${{a}_{3}}^{2}+2{a}_{3}{a}_{5}+{{a}_{5}}^{2}=25$,又an>0,∴a3+a5=5,①…(2分)
又2为a3与a5的等比中项,∴a3a5=4,②
又q∈(0,1),∴a3>a5,
∴联立①②,解得a3=4,a5=1,
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=4}\\{{a}_{1}{{q}^{4}}_{\;}=1}\end{array}\right.$,由q∈(0,1)解得$q=\frac{1}{2},{a}_{1}=16$,…(4分)
∴${a}_{n}=16×(\frac{1}{2})^{n-1}$=25-n,
∴bn=5-log2an=5-(5-n)=n.…(6分)
(2)解:∵$\frac{1}{{b}_{n}{b}_{n+2}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$.…(8分)
∴${S}_{n}=\frac{1}{{b}_{1}{b}_{3}}+\frac{1}{{b}_{2}{b}_{4}}+…+\frac{1}{{b}_{n}{b}_{n+2}}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{n}-\frac{1}{n+2}$)
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}-\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{1}{2}(\frac{1}{n+1}+\frac{1}{n+2})$.…(12分)
点评 本题考查数列的通项公式和前n项和公式的求法,是中档题,解题时要认真审题,注意等比数列的性质和裂项求和法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,10] | B. | (-∞,10) | C. | (10,+∞) | D. | [10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | kπ+$\frac{π}{2}$(k∈Z) | B. | kπ(k∈Z) | C. | 2kπ+$\frac{π}{2}$(k∈Z) | D. | $\frac{1}{2}kπ$(k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
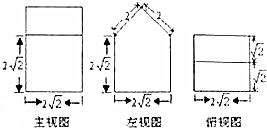
| A. | 16$\sqrt{2}$cm3 | B. | 32$\sqrt{2}$cm3 | C. | 24$\sqrt{2}$cm3 | D. | 20$\sqrt{2}$cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°,点H,G分别是线段EF,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,抛物线的方程为y2=2px(p>0),F为该抛物线的焦点,A是该抛物线的准线与x轴的交点,M是抛物线上一点,且满足MA⊥MF.
如图,抛物线的方程为y2=2px(p>0),F为该抛物线的焦点,A是该抛物线的准线与x轴的交点,M是抛物线上一点,且满足MA⊥MF.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com