
【题目】已知椭圆![]() 和圆
和圆![]() ,
,![]() 、
、![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(I)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 与椭圆
与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】2016年春节期间全国流行在微信群里发抢红包,现假设某人将688元发成手气红包50个,产生的手气红包频数分布表如下:
金额分组 |
|
|
|
|
|
|
频 数 | 3 | 9 | 17 | 11 | 8 | 2 |
(1)求产生的手气红包的金额不小于9元的频率;
(2)估计手气红包金额的平均数(同一组中的数据用该组区间的中点值作代表);
(3)在这50个红包组成的样本中,将频率视为概率.
①若红包金额在区间![]() 内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
内为最佳运气手,求抢得红包的某人恰好是最佳运气手的概率;
②随机抽取手气红包金额在![]() 内的两名幸运者,设其手气金额分别为
内的两名幸运者,设其手气金额分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PA∥CE,AB=CE![]() PA,PA⊥平面ABCD.
PA,PA⊥平面ABCD.
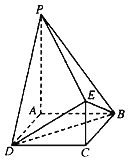
(1)证明:PE⊥平面DBE;
(2)求二面角B﹣PD﹣E的正弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数是简化繁杂运算的产物.16世纪时,为了简化数值计算,数学家希望将乘除法归结为简单的加减法.当时已经有数学家发现这在某些情况下是可以实现的.
比如,利用以下2的次幂的对应表可以方便地算出![]() 的值.
的值.
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 |
首先,在第二行找到16与256;然后找出它们在第一行对应的数,即4与8,并求它们的和,即12;最后在第一行中找到12,读出其对应的第二行中的数4096,这就是![]() 的值.
的值.
用类似的方法可以算出![]() 的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是
的值,首先,在第二行找到4096与128;然后找出它们在第一行对应的数,即12与7,并求它们的______;最后在第一行中找到______,读出其对应的第二行中的数______,这就是![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是坐标原点,椭圆
是坐标原点,椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,点
,点![]() 在椭圆上,若
在椭圆上,若![]() 的面积最大时
的面积最大时![]() 且最大面积为
且最大面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() :
:![]() 与椭圆
与椭圆![]() 在第一象限交于点
在第一象限交于点![]() ,点
,点![]() 是第四象限内的点且在椭圆
是第四象限内的点且在椭圆![]() 上,线段
上,线段![]() 被直线
被直线![]() 垂直平分,直线
垂直平分,直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加某个知识答题游戏节目,答题分两轮,第一轮为“选题答题环节”第二轮为“轮流坐庄答题环节”.首先进行第一轮“选题答题环节”,答题规则是:每位同学各自从备选的5道不同题中随机抽出3道题进行答题,答对一题加10分,答错一题(不答视为答错)减5分,已知甲能答对备选5道题中的每道题的概率都是![]() ,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第
,乙恰能答对备选5道题中的其中3道题;第一轮答题完毕后进行第二轮“轮流坐庄答题环节”,答题规则是:先确定一人坐庄答题,若答对,继续答下一题…,直到答错,则换人(换庄)答下一题…以此类推.例如若甲首先坐庄,则他答第1题,若答对继续答第2题,如果第2题也答对,继续答第3题,直到他答错则换成乙坐庄开始答下一题,…直到乙答错再换成甲坐庄答题,依次类推两人共计答完20道题游戏结束,假设由第一轮答题得分期望高的同学在第二轮环节中最先开始作答,且记第![]() 道题也由该同学(最先答题的同学)作答的概率为
道题也由该同学(最先答题的同学)作答的概率为![]() (
(![]() ),其中
),其中![]() ,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是
,已知供甲乙回答的20道题中,甲,乙两人答对其中每道题的概率都是![]() ,如果某位同学有机会答第
,如果某位同学有机会答第![]() 道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
道题且回答正确则该同学加10分,答错(不答视为答错)则减5分,甲乙答题相互独立;两轮答题完毕总得分高者胜出.回答下列问题
(1)请预测第二轮最先开始作答的是谁?并说明理由
(2)①求第二轮答题中![]() ,
,![]() ;
;
②求证![]() 为等比数列,并求
为等比数列,并求![]() (
(![]() )的表达式.
)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校实行新课程改革,即除语、数、外三科为必考科目外,还要在理、化、生、史、地、政六科中选择三科作为选考科目.已知某生的高考志愿为某大学环境科学专业,按照该大学上一年高考招生选考科目要求理、化必选,为该生安排课表(上午四节、下午四节,每门课每天至少一节),已知该生某天最后两节为自习课,且数学不排下午第一节,语文、外语不相邻(上午第四节和下午第一节不算相邻),则该生该天课表有( ).
A.444种B.1776种C.1440种D.1560种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com