
分析 通过$\overrightarrow{A{F}_{1}}$•$\overrightarrow{A{F}_{2}}$=0可知AF1⊥AF2,通过设F2M=5x,则MA=4x,利用△F2OM∽△F2AF1可知x=$\frac{\sqrt{10}}{15}$c,通过椭圆定义可知F1A=2a-$\frac{3\sqrt{10}}{5}$c,利用勾股定理可知${F}_{1}{{F}_{2}}^{2}$=${F}_{1}{A}^{2}$+${F}_{2}{A}^{2}$,进而计算可得结论.
解答 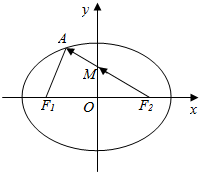 解:依题意,不妨设点A在第二象限,
解:依题意,不妨设点A在第二象限,
∵$\overrightarrow{A{F}_{1}}$•$\overrightarrow{A{F}_{2}}$=0,
∴AF1⊥AF2,
∵$\overrightarrow{{F}_{2}M}$=$\frac{5}{4}$$\overrightarrow{MA}$,
∴设F2M=5x,则MA=4x,
∵△F2OM∽△F2AF1,
∴$\frac{{F}_{2}M}{{F}_{2}{F}_{1}}$=$\frac{{F}_{2}O}{{F}_{2}A}$,即$\frac{5x}{2c}$=$\frac{c}{9x}$,
化简得:x=$\frac{\sqrt{10}}{15}$c,
∴F2A=9x=$\frac{3\sqrt{10}}{5}$c,
由椭圆定义可知F1A=2a-F2A=2a-$\frac{3\sqrt{10}}{5}$c,
由勾股定理可知:${F}_{1}{{F}_{2}}^{2}$=${F}_{1}{A}^{2}$+${F}_{2}{A}^{2}$,
即4c2=(2a-$\frac{3\sqrt{10}}{5}$c)2+($\frac{3\sqrt{10}}{5}$c)2,
化简得:4c2-$3\sqrt{10}$ac+5a2=0,
∴4e2-$3\sqrt{10}$e+5=0,
解得:e=$\frac{3\sqrt{10}±\sqrt{(3\sqrt{10})^{2}-4×4×5}}{2×4}$=$\frac{3\sqrt{10}±\sqrt{10}}{8}$,
又∵0<e<1,
∴e=$\frac{3\sqrt{10}-\sqrt{10}}{8}$=$\frac{\sqrt{10}}{4}$,
故答案为:$\frac{\sqrt{10}}{4}$.
点评 本题考查椭圆的简单性质,考查运算求解能力,利用相似三角形及勾股定理是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{8}$ | B. | $\frac{13}{8}$ | C. | $\frac{8}{11}$ | D. | $\frac{8}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.
如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
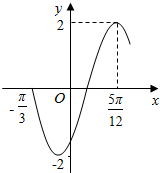 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则这个函数的周期和初相分别是( )| A. | 2,-$\frac{π}{3}$ | B. | 2,-$\frac{π}{6}$ | C. | π,-$\frac{π}{6}$ | D. | π,-$\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com