
【题目】小王在年初用50万元购买一辆大货车,第一年因缴纳各种费用需支出6万元,从第二年起,每年都比上一年增加支出2万元,假定该车每年的运输收入均为25万元.小王在该车运输累计收入超过总支出后,考虑将大货车作为二手车出售,若该车在第x年年底出售,其销售价格为25-x万元(国家规定大货车的报废年限为10年).
(1)大货车运输到第几年年底,该车运输累计收入超过总支出?
(2)在第几年年底将大货车出售,能使小王获得的年平均利润最大(利润=累计收入+销售收入-总支出)?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2+mx+n(m、n∈R)的两个零点分别在(0,1)与(1,2)内,则(m+1)2+(n﹣2)2的取值范围是( )
A.![]()
B.![]()
C.[2,5]
D.(2,5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱柱ABCD﹣A1B1C1D1中,底面ABCD是边长为3的正方形,侧棱AA1长为4,且AA1与A1B1 , A1D1的夹角都是60°,则AC1的长等于( ) 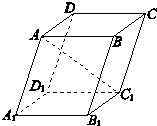
A.10
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=(﹣2m2+m+2)xm+1为偶函数.
(1)求f(x)的解析式;
(2)若函数y=f(x)﹣2(a﹣1)x+1在区间(2,3)上为单调函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)的零点与g(x)=4x+2x﹣2的零点之差的绝对值不超过0.25,则f(x)可以是( )
A.f(x)=4x﹣1
B.f(x)=(x﹣1)2
C.f(x)=ex﹣1
D.f(x)=ln(x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|lgx|.若a≠b且,f(a)=f(b),则a+b的取值范围是( )
A.(1,+∞)
B.[1,+∞)
C.(2,+∞)
D.[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)请根据对数函数![]() 来指出函数
来指出函数![]() 的基本性质(结论不要求证明),并画出图像;
的基本性质(结论不要求证明),并画出图像;
(2)拉普拉斯称赞对数是一项“使天文学家寿命倍増”的发明.对数可以将大数之间的乘除运算简化为加减运算,请证明: ![]() ;
;
(3)2017年5月23日至27日,围棋世界冠军柯洁与DeepMind公司开发的程序“AlphaGo”进行三局人机对弈,以复杂的围棋来测试人工智能.围棋复杂度的上限约为![]() ,而根据有关资料,可观测宇宙中普通物质的原子总数约为
,而根据有关资料,可观测宇宙中普通物质的原子总数约为![]() .甲、乙两个同学都估算了
.甲、乙两个同学都估算了![]() 的近似值,甲认为是
的近似值,甲认为是![]() ,乙认为是
,乙认为是![]() .现有两种定义:
.现有两种定义:
①若实数![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]() ;
;
②若实数![]() ,且
,且![]() ,满足
,满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]() ;请你任选取其中一种定义来判断哪个同学的近似值更接近
;请你任选取其中一种定义来判断哪个同学的近似值更接近![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)+g(x)=3x .
(1)求 f(x),g(x);
(2)若对于任意实数t∈[0,1],不等式f(2t)+ag(t)<0恒成立,求实数a的取值范围;
(3)若存在m∈[﹣2,﹣1],使得不等式af(m)+g(2m)<0成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com