【题目】已知
是首项为19，公差为-2的等差数列，
为
的前
项和．
（1）求通项
及
；
（2）设
是首项为1，公比为3的等比数列，求数列
的通项公式及其前
项和
．
手拉手全优练考卷系列答案科目：高中数学 来源： 题型：
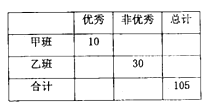
【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩后，得到如下的列联表.
已知从全部105人中随机抽取1人为优秀的概率为
.
（1）请完成上面的列联表：若按
的可靠性要求，根据列联表的数据，能否认为“成绩与班级有关系”；
（2）若按下面的方法从甲班优秀的学生中抽取一人：把甲班优秀的10名学生从2到11进行编号，先后两次抛掷一枚均匀的骰子，出现的点数之和为被抽取人的序号.试求抽到10号的概率.
附：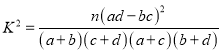 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正方体
的棱长为1， 
分别是棱
的中点，过直线
的平面分别与棱
交于
，设
, 
，给出以下四个命题：
①
②当且仅当
时，四边形
的面积最小；
③四边形
周长
, 
，则
是奇函数；
④四棱锥
的体积
为常函数；
其中正确命题的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某出租车公司响应国家节能减排的号召，已陆续购买了140辆纯电动汽车作为运营车辆，目前我国主流纯电动汽车按续航里程数
．（单位：公里）分为3类，即
类：
，
类：
， 
类：
，该公司对这140辆车的行驶总里程进行统计，结果如下表：
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
（1）从这140辆汽车中任取一辆，求该车行驶总里程超过10万公里的概率；
（2）公司为了了解这些车的工作状况，决定抽取了14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从
类车中抽取了
辆车．
①求
的值；
②如果从这
辆车中随机选取两辆车，求恰有一辆车行驶总里程超过10万公里的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将五个1，五个2，五个3，五个4，五个5共25个数填入一个5行5列的表格内（每格填入一个数），使得同一行中任何两数之差的绝对值不超过2，考查每行中五个数之和，记这五个和的最小值为
，则
的最大值为（ ）
A. 
B. 9 C. 10 D. 11
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若要得到函数y=sin（2x﹣ 
）的图象，可以把函数y=sin2x的图象（ ）
A.向右平移 
个单位
B.向左平移 个单位
C.向右平移 个单位
D.向左平移 个单位
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（2cosωx，cos2ωx）， 
=（sinωx，1）（其中ω＞0），令f（x）= 
，且f（x）的最小正周期为π．
（1）求 
的值；
（2）写出 
上的单调递增区间．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知公比为负值的等比数列{an}中，a1a5=4，a4=﹣1．
（1）求数列{an}的通项公式；
（2）设bn= 
+ 
+…+ 
，求数列{an+bn}的前n项和Sn ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
