
【题目】已知函数 ![]() ,则函数y=f(x)的大致图象为( )
,则函数y=f(x)的大致图象为( )
A.
B.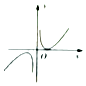
C.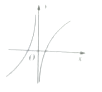
D.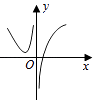
【答案】D
【解析】解:由题意可得函数的定义域为(﹣∞,0)∪(0,+∞),
函数 ![]() ,可得f(﹣x)≠±f(x),
,可得f(﹣x)≠±f(x),
故函数为非奇非偶函数,排除:B、C;
当x>0时,函数 ![]() =x2﹣
=x2﹣ ![]() ,f′(x)=2x﹣
,f′(x)=2x﹣ ![]() =
= ![]() ,
,
令g(x)=x3+1﹣lnx,(x>0),
g′(x)=3x2﹣ ![]() =
= ![]() ,
,
令g′(x)=0,解得x= ![]() ,
,
故当0<x< ![]() 时,g′(x)<0,g(x)是减函数,
时,g′(x)<0,g(x)是减函数,
x> ![]() 时,函数g(x)是单调递增,g(x)的最小值为g(
时,函数g(x)是单调递增,g(x)的最小值为g( ![]() )=
)= ![]() >0,
>0,
∴f′(x)>0在x>0时,恒成立,函数是单调增函数,排除A;
综上可得选项D符合题意,
故答案为:D.
根据函数的解析式,得出函数的定义域,先判断出函数非奇非偶,图象即不关于原点对称也不关于y轴对称,再对函数求导,找到函数的单调区间即可判断出函数图象.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】已知点(2,3)在椭圆 ![]() 上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为
上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为 ![]() .
.
(I)求椭圆C的方程;
(II)设M(x1 , y1),N(x2 , y2)(x1≠x2)为椭圆上的两点,且满足 ![]()
![]() =
= ![]() ,求证:△MON的面积为定值,并求出这个定值.
,求证:△MON的面积为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点P(1,﹣2),直线l: ![]() (m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(m 为参数),以坐标原点为极点,以 x轴的正半轴为极轴建立极坐标系;曲线C的极坐标方程为ρsin2θ=3cosθ;直线l与曲线C的交点为A,B.
(1)求直线l和曲线C的普通方程;
(2)求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos2(ωx+φ)+1(A>0,ω>0,0<φ< ![]() )的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
)的最大值为3,f(x)的图象与y轴的交点坐标为(0,2),其相邻两条对称轴间的距离为2,则f(1)+f(2)+f(3)+…+f(2016)的值为( )
A.2468
B.3501
C.4032
D.5739
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知曲线 ![]() (α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线
(α为参数),在以O为极点,x轴正半轴为极轴的极坐标系中,曲线 ![]() ,曲线C3:ρ=2sinθ.
,曲线C3:ρ=2sinθ.
(1)求曲线C1与C2的交点M的直角坐标;
(2)设点A,B分别为曲线C2 , C3上的动点,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F(1,0),直线l:x=﹣1,直线l'垂直l于点P,线段PF的垂直平分线交l'于点Q.
(1)求点Q的轨迹方程C;
(2)过F做斜率为 ![]() 的直线交C于A,B,过B作l平行线交C于D,求△ABD外接圆的方程.
的直线交C于A,B,过B作l平行线交C于D,求△ABD外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四面体A﹣BCD中,AB=CD=10,AC=BD=2 ![]() ,AD=BC=2
,AD=BC=2 ![]() ,则四面体A﹣BCD外接球的表面积为( )
,则四面体A﹣BCD外接球的表面积为( )
A.50π
B.100π
C.200π
D.300π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 在x1处取得极大值,在x2处取得极小值,满足x1∈(﹣1,0),x2∈(0,1),则
在x1处取得极大值,在x2处取得极小值,满足x1∈(﹣1,0),x2∈(0,1),则 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.(0,1)
C.![]()
D.[1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com