
【题目】在数列{an}中,已知a1=2,an+1=3an+2n﹣1.
(1)求证:数列{an+n}为等比数列;
(2)记bn=an+(1﹣λ)n,且数列{bn}的前n项和为Tn , 若T3为数列{Tn}中的最小项,求λ的取值范围.
【答案】
(1)证明:∵an+1=3an+2n﹣1,
∴an+1+n+1=3(an+n).
又a1=2,
∴an>0,an+n>0,
故 ![]() ,
,
∴{an+n}是以3为首项,公比为3的等比数列
(2)由(1)知道 ![]() ,bn=an+(1﹣λ)n,
,bn=an+(1﹣λ)n,
∴ ![]() .
.
∴ ![]() .
.
若T3为数列{Tn}中的最小项,则对n∈N*有 ![]() 恒成立,
恒成立,
即3n+1﹣81≥(n2+n﹣12)λ对n∈N*恒成立
1°当n=1时,有 ![]() ;
;
2°当n=2时,有T2≥T3λ≥9;
3°当n≥4时,n2+n﹣12=(n+4)(n﹣3)>0恒成立,
∴ ![]() 对n≥4恒成立.
对n≥4恒成立.
令 ![]() ,则
,则 ![]() 对n≥4恒成立,
对n≥4恒成立,
∴ ![]() 在n≥4时为单调递增数列.
在n≥4时为单调递增数列.
∴λ≤f(4),即 ![]() .
.
综上, ![]()
【解析】(1)由an+1=3an+2n﹣1,整理得:an+1+n+1=3(an+n).由an+n>0, ![]() ,可知{an+n}是以3为首项,公比为3的等比数列;(2)由(1)求得数列{bn}通项公式及前n项和为Tn , 由T3为数列{Tn}中的最小项,则对n∈N*有
,可知{an+n}是以3为首项,公比为3的等比数列;(2)由(1)求得数列{bn}通项公式及前n项和为Tn , 由T3为数列{Tn}中的最小项,则对n∈N*有 ![]() 恒成立,分类分别求得当n=1时和当n=2λ的取值范围, 当n≥4时,
恒成立,分类分别求得当n=1时和当n=2λ的取值范围, 当n≥4时, ![]() ,利用做差法,根据函数的单调性,即可求得λ的取值范围.
,利用做差法,根据函数的单调性,即可求得λ的取值范围.
【考点精析】关于本题考查的数列的前n项和和数列的通项公式,需要了解数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,①![]() 的一个充要条件是
的一个充要条件是![]() 与它的共轭复数相等:
与它的共轭复数相等:
②利用独立性检验来考查两个分类变量![]() ,
,![]() 是否有关系,当随机变量
是否有关系,当随机变量![]() 的观测值
的观测值![]() 值越大,“
值越大,“![]() 与
与![]() 有关系”成立的可能性越大;
有关系”成立的可能性越大;
③在回归分析模型中,若相关指数越大,则残差平方和越小,模型的拟合效果越好;
④若![]() ,
,![]() 是两个相等的实数,则
是两个相等的实数,则![]() 是纯虚数;
是纯虚数;
⑤某校高三共有![]() 个班,
个班,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,由此推测各班都超过
人,由此推测各班都超过![]() 人,这个推理过程是演绎推理.
人,这个推理过程是演绎推理.
其中真命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家质量监督检验检疫局于2004年5月31日发布了新的![]() 车辆驾驶人员血液、呼气酒精含量阀值与检验
车辆驾驶人员血液、呼气酒精含量阀值与检验![]() 国家标准
国家标准![]() 新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克
新标准规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克![]() 百毫升,小于80毫克
百毫升,小于80毫克![]() 百毫升为饮酒驾车,血液中的酒精含量大于或等于80毫克
百毫升为饮酒驾车,血液中的酒精含量大于或等于80毫克![]() 百毫升为醉酒驾车
百毫升为醉酒驾车![]() 经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如图:
经过反复试验,喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如图:

该函数近似模型如下: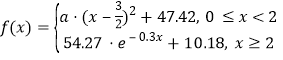 ,又已知刚好过1小时时测得酒精含量值为
,又已知刚好过1小时时测得酒精含量值为![]() 毫克
毫克![]() 百毫升
百毫升![]() 根据上述条件,回答以下问题:
根据上述条件,回答以下问题:
![]() 试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值?最大值是多少?
试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值?最大值是多少?
![]() 试计算喝一瓶啤酒后多少小时后才可以驾车?
试计算喝一瓶啤酒后多少小时后才可以驾车?![]() 时间以整小时计算
时间以整小时计算![]()
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:![]() )的分组区间为
)的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
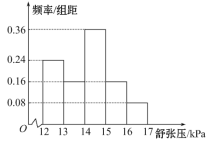
,![]() ,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有
,将其按从左到右的顺序分别编号为第一组,第二组,......,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有![]() 人,第三组中没有疗效的有
人,第三组中没有疗效的有![]() 人,则第三组中有疗效的人数为( )
人,则第三组中有疗效的人数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com