
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;③命题“
”;③命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题是( )
”的充要条件.其中正确的命题是( )
A.②③④B.①③④C.①②④D.①②③
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)过椭圆 上异于其顶点的任意一点Q作圆
上异于其顶点的任意一点Q作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 不在坐标轴上),若直线
不在坐标轴上),若直线![]() 在x轴,y轴上的截距分别为
在x轴,y轴上的截距分别为![]() ,证明:
,证明:![]() 为定值;
为定值;
(3)若![]() 是椭圆
是椭圆![]() 上不同两点,
上不同两点,![]() 轴,圆E过
轴,圆E过![]() ,且椭圆
,且椭圆![]() 上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆
上任意一点都不在圆E内,则称圆E为该椭圆的一个内切圆,试问:椭圆![]() 是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
是否存在过焦点F的内切圆?若存在,求出圆心E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织了垃圾分类知识竞赛活动.设置了四个箱子,分别写有“厨余垃圾”、“有害垃圾”、“可回收物”、“其它垃圾”;另有卡片若干张,每张卡片上写有一种垃圾的名称.每位参赛选手从所有卡片中随机抽取![]() 张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得
张,按照自己的判断,将每张卡片放入对应的箱子中.按规则,每正确投放一张卡片得![]() 分,投放错误得
分,投放错误得![]() 分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得
分.比如将写有“废电池”的卡片放入写有“有害垃圾”的箱子,得![]() 分,放入其它箱子,得
分,放入其它箱子,得![]() 分.从所有参赛选手中随机抽取
分.从所有参赛选手中随机抽取![]() 人,将他们的得分按照
人,将他们的得分按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组,绘成频率分布直方图如图:
分组,绘成频率分布直方图如图:
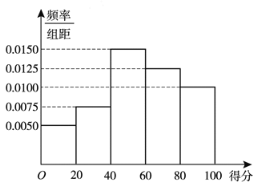
(1)分别求出所抽取的![]() 人中得分落在组
人中得分落在组![]() 和
和![]() 内的人数;
内的人数;
(2)从所抽取的![]() 人中得分落在组
人中得分落在组![]() 的选手中随机选取
的选手中随机选取![]() 名选手,以
名选手,以![]() 表示这
表示这![]() 名选手中得分不超过
名选手中得分不超过![]() 分的人数,求
分的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3) 如果某选手将抽到的20张卡片逐一随机放入四个箱子,能否认为该选手不会得到100分?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于工作需要,某公司准备一次性购买两台具有智能打印、扫描、复印等多种功能的智能激光型打印机.针对购买后未来五年内的售后,厂家提供如下两种方案:
方案一:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元;
元;
方案二:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元.
元.
该公司搜集并整理了![]() 台这款打印机使用五年的维修次数,所得数据如下表所示:
台这款打印机使用五年的维修次数,所得数据如下表所示:
维修次数 |
|
|
|
|
台数 |
|
|
|
|
以这![]() 台打印机使用五年的维修次数的频率代替
台打印机使用五年的维修次数的频率代替![]() 台打印机使用五年的维修次数的概率,记
台打印机使用五年的维修次数的概率,记![]() 表示这两台智能打印机五年内共需维修的次数.
表示这两台智能打印机五年内共需维修的次数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以两种方案产生的维修费用的期望值为决策依据,写出你的选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于
的长轴是短轴的两倍,以短轴一个顶点和长轴一个顶点为端点的线段作直径的圆的周长等于![]() ,直线l与椭圆C交于
,直线l与椭圆C交于![]() 两点.
两点.
(1)求椭圆C的方程;
(2)过点O作直线l的垂线,垂足为D.若![]() ,求动点D的轨迹方程.
,求动点D的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商贸公司售卖某种水果.经市场调研可知:在未来![]() 天内,这种水果每箱的销售利润
天内,这种水果每箱的销售利润![]() (单位:元)与时间
(单位:元)与时间![]() ,单位:天)之间的函数关系式为
,单位:天)之间的函数关系式为![]() , 且日销售量
, 且日销售量![]() (单位:箱)与时间
(单位:箱)与时间![]() 之间的函数关系式为
之间的函数关系式为![]()
①第![]() 天的销售利润为__________元;
天的销售利润为__________元;
②在未来的这![]() 天中,公司决定每销售
天中,公司决定每销售![]() 箱该水果就捐赠
箱该水果就捐赠![]() 元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间
元给 “精准扶贫”对象.为保证销售积极性,要求捐赠之后每天的利润随时间![]() 的增大而增大,则
的增大而增大,则![]() 的最小值是__________.
的最小值是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
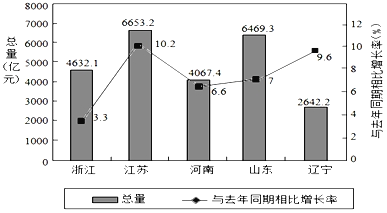
A.2017年第一季度GDP增速由高到低排位第5的是浙江省.
B.与去年同期相比,2017年第一季度的GDP总量实现了增长.
C.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
D.去年同期河南省的GDP总量不超过4000亿元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),它与曲线
(t为参数),它与曲线
C:(y-2)2-x2=1交于A、B两点.
(1)求|AB|的长;
(2)在以O为极点,x轴的正半轴为极轴建立极坐标系,设点P的极坐标为![]() ,求点P到线段AB中点M的距离.
,求点P到线段AB中点M的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com