
分析 (1)直接利用等差中项的概念结合已知数列{an}是等差数列证明;
(2)直接利用定义结合已知数列{an}是等比数列证明.
解答 证明:(1)∵S1=a1+a2+…+an,S2=an+1+an+2+…+a2n,S3=a2n+1+a2n+2+…+a3n.
则2S2=2(an+1+an+2+…+a2n),
S1+S3=(a1+a2+…+an)+(a2n+1+a2n+2+…+a3n)=(a1+a2n+1+a2+a2n+2+…+an+a3n),
∵数列{an}是等差数列,∴由等差数列的性质得(a1+a2n+1+a2+a2n+2+…+an+a3n)=2(an+1+an+2+…+a2n),
即2S2=S1+S3,∴数列S1,S2,S3也是等差数列;
(2)若数列{an}是等比数列,则$\frac{{S}_{2}}{{S}_{1}}=\frac{{a}_{n+1}+{a}_{n+2}+…+{a}_{2n}}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{{q}^{n}({a}_{1}+{a}_{2}+…+{a}_{n})}{{a}_{1}+{a}_{2}+…+{a}_{n}}={q}^{n}$,
$\frac{{S}_{3}}{{S}_{2}}=\frac{{a}_{2n+1}+{a}_{2n+2}+…+{a}_{3n}}{{a}_{n+1}+{a}_{n+2}+…+{a}_{2n}}$=$\frac{{q}^{n}({a}_{n+1}+{a}_{n+2}+…+{a}_{2n})}{{a}_{n+1}+{a}_{n+2}+…+{a}_{2n}}={q}^{n}$,
∴数列S1,S2,S3也是等比数列.
点评 本题考查等差数列和等比数列的性质,关键是熟记性质并用来解决问题,是基础题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
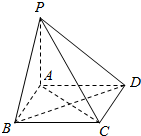 如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )
如图所示,四边形ABCD为正方形,PA⊥平面ABCD,则在平面PAB,平面PAD,平面PCD,平面PBC及平面ABCD中,互相垂直的有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3}{2}π$ | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com