
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
【答案】C
【解析】
对四个结论逐一分析判断,
对于①,利用翻折前后![]() 这个条件不变,易得
这个条件不变,易得![]() 平面
平面![]() ,从而
,从而![]() ;
;
对于②,当平面![]() 平面
平面![]() 时,四面体ABCD的体积最大,易得出体积;
时,四面体ABCD的体积最大,易得出体积;
对于③,当平面![]() 平面
平面![]() 时,BC与平面ABD所成的角最大,即
时,BC与平面ABD所成的角最大,即![]() ,计算其正弦值可得出结果;
,计算其正弦值可得出结果;
对于④,在翻折的过程中,BD的中点到四面体四个顶点的距离均相等,所以外接球的直径恒为BD,体积恒为定值.
如图,当![]() 时,∵
时,∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴
,∴![]() ,即①正确;
,即①正确;

当平面![]() 平面
平面![]() 时,四面体ABCD的体积最大,最大值为
时,四面体ABCD的体积最大,最大值为![]() ,即②正确;
,即②正确;
当平面![]() 平面
平面![]() 时,BC与平面ABD所成的角最大,为
时,BC与平面ABD所成的角最大,为![]() ,而
,而![]() ,
,
∴BC与平面ABD所成角一定小于![]() ,即③错误;
,即③错误;
在翻折的过程中,![]() 和
和![]() 始终是直角三角形,斜边都是BD,其外接球的球心永远是BD的中点,外接球的直径为BD,
始终是直角三角形,斜边都是BD,其外接球的球心永远是BD的中点,外接球的直径为BD,
∴四面体ABCD的外接球的体积不变,即④正确.
故正确的有①②④.
故选:C.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】一个口袋中装有大小相同的5个小球,编号分别为0,1,2,3,4,现从中随机地摸一个球,记下编号后放回,连摸3次,若摸出的3个小球的最大编号与最小编号之差为2,则共有________种不同的摸球方法(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在实数k,b,使得函数![]() 和
和![]() 对其定义域上的任意实数x同时满足:
对其定义域上的任意实数x同时满足:![]() 且
且![]() ,则称直线:
,则称直线:![]() 为函数
为函数![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() (其中e为自然对数的底数).试问:
(其中e为自然对数的底数).试问:
(1)函数![]() 和
和![]() 的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
的图象是否存在公共点,若存在,求出交点坐标,若不存在,说明理由;
(2)函数![]() 和
和![]() 是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
是否存在“隔离直线”?若存在,求出此“隔离直线”的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上的点
上的点![]() 到焦点的距离为
到焦点的距离为![]() .
.

(1)求![]() 的值;
的值;
(2)如上图,已知动线段![]() (
(![]() 在
在![]() 的右边)在直线
的右边)在直线![]() 上,且
上,且![]() ,现过
,现过![]() 作
作![]() 的切线,取左边的切点
的切线,取左边的切点![]() ,过
,过![]() 作
作![]() 的切线,取右边的切点为
的切线,取右边的切点为![]() ,当
,当![]() ,求
,求![]() 点的横坐标
点的横坐标![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了A,B两种小区管理方案,为了决定选取哪种方案为小区的最终管理方案,随机选取了4名物业人员进行投票,物业人员投票的规则如下:①单独投给A方案,则A方案得1分,B方案得﹣1分;②单独投给B方案,则B方案得1分,A方案得﹣1分;③弃权或同时投票给A,B方案,则两种方案均得0分.前1名物业人员的投票结束,再安排下1名物业人员投票,当其中一种方案比另一种方案多4分或4名物业人员均已投票时,就停止投票,最后选取得分多的方案为小区的最终管理方案.假设A,B两种方案获得每1名物业人员投票的概率分别为![]() 和
和![]() .
.
(1)在第1名物业人员投票结束后,A方案的得分记为ξ,求ξ的分布列;
(2)求最终选取A方案为小区管理方案的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,
(x∈R,实数a∈[0,+∞),e=2.71828…是自然对数的底数,![]() ).
).
(Ⅰ)若f(x)≥0在x∈R上恒成立,求实数a的取值范围;
(Ⅱ)若ex≥lnx+m对任意x>0恒成立,求证:实数m的最大值大于2.3.
查看答案和解析>>
科目:高中数学 来源: 题型:
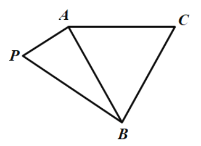
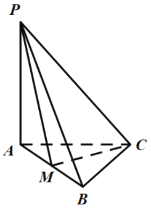
【题目】如图所示,平面四边形![]() 中,
中,![]() 为直角,
为直角,![]() 为等边三角形,现把
为等边三角形,现把![]() 沿着
沿着![]() 折起,使得平面
折起,使得平面![]() 与平面
与平面![]() 垂直,且点M为
垂直,且点M为![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com