
【题目】已知函数 ![]() .
.
(1)求函数 ![]() 在
在 ![]() 处的切线方程;
处的切线方程;
(2)设 ![]() ,讨论函数
,讨论函数 ![]() 的零点个数.
的零点个数.
【答案】(1) ![]() l;(2) 当
l;(2) 当![]() 时,有
时,有 ![]() 个零点;
个零点; ![]() ,
, ![]() 个零点;
个零点; ![]() ,没有零点;所以
,没有零点;所以 ![]() ,零点
,零点 ![]() 个;
个; ![]() ,零点
,零点 ![]() 个;
个; ![]() ,零点
,零点 ![]() 个.
个.
【解析】试题分析:(1)求函数 ![]() 在
在 ![]() 处的切线方程,应先求其导函数
处的切线方程,应先求其导函数![]() ,在
,在 ![]() 处的切线的斜率就是该点处的导函数值
处的切线的斜率就是该点处的导函数值![]() ,用直线方程的点斜式可得切线的方程;
,用直线方程的点斜式可得切线的方程; ![]()
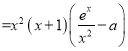 ,因为
,因为![]() ,所以考虑函数
,所以考虑函数![]() 的零点个数就是考虑函数
的零点个数就是考虑函数![]() 的零点个数问题,构造函数
的零点个数问题,构造函数![]() ,求导数
,求导数![]() ,解不等式
,解不等式![]() ,得函数在
,得函数在 ![]() 上单调递减,
上单调递减, ![]() 上单调递增,求得其在
上单调递增,求得其在![]() 函数取得极小值
函数取得极小值 ![]() .根据函数
.根据函数![]() 图像、直线
图像、直线![]() 及
及![]() 的取值情况可得,当
的取值情况可得,当![]() 时,有
时,有 ![]() 个零点;
个零点; ![]() ,
, ![]() 个零点;
个零点; ![]() ,没有零点.
,没有零点.
试题解析:(1) ![]() ,
, ![]() ,
,
所以函数 ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() ,即
,即 ![]() .
.
(2) ![]() ,
, ![]() ,可得
,可得 ![]() ,
,
设 ![]() ,则
,则 ![]() ,函数在
,函数在 ![]() 上单调递减,
上单调递减, ![]() 上单调递增,
上单调递增,
所以 ![]() 函数取得极小值
函数取得极小值 ![]() .
.
由函数![]() 图像、直线
图像、直线![]() 及
及![]() 的取值情况可得,
的取值情况可得,
当![]() 时,有
时,有 ![]() 个零点;
个零点; ![]() ,
, ![]() 个零点;
个零点; ![]() ,没有零点.
,没有零点.
所以 ![]() ,零点
,零点 ![]() 个;
个; ![]() ,零点
,零点 ![]() 个;
个; ![]() ,零点
,零点 ![]() 个.
个.


科目:高中数学 来源: 题型:
【题目】不等式|x﹣ ![]() ≤
≤ ![]() 的解集为{x|n≤x≤m}
的解集为{x|n≤x≤m}
(1)求实数m,n;
(2)若实数a,b满足:|a+b|<m,|2a﹣b|<n,求证:|b|< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={m|m∈Z,且|m|≤2018},M的子集S满足:对S中任意3个元素a,b,c(不必不同),都有a+b+c≠0.求集合S的元素个数的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设首项为1的正项数列{an}的前n项和为Sn , 且Sn+1﹣3Sn=1.
(1)求证:数列{an}为等比数列;
(2)数列{an}是否存在一项ak , 使得ak恰好可以表示为该数列中连续r(r∈N* , r≥2)项的和?请说明理由;
(3)设 ![]() ,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
,试问是否存在正整数p,q(1<p<q)使b1 , bp , bq成等差数列?若存在,求出所有满足条件的数组(p,q);若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
(1)设f(x)与g(x)是定义在R上的两个函数,若|f(x1)+f(x2)|≥|g(x1)+g(x2)|恒成立,且f(x)为奇函数,则g(x)也是奇函数;
(2)若x1 , x2∈R,都有|f(x1)﹣f(x2)|>|g(x1)﹣g(x2)|成立,且函数f(x)在R上递增,则f(x)+g(x)在R上也递增;
(3)已知a>0,a≠1,函数f(x)= ![]() ,若函数f(x)在[0,2]上的最大值比最小值多
,若函数f(x)在[0,2]上的最大值比最小值多 ![]() ,则实数a的取值集合为
,则实数a的取值集合为 ![]() ;
;
(4)存在不同的实数k,使得关于x的方程(x2﹣1)2﹣|x2﹣1|+k=0的根的个数为2个、4个、5个、8个.则所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①已知命题p:x∈R,tanx=2;命题q:x∈R,x2﹣x+1≥0,则命题p∧q是真命题;
②过点(﹣1,2)且在x轴和y轴上的截距相等的直线方程是x+y﹣1=0;
③函数f(x)=2x+2x﹣3在定义域内有且只有一个零点;
④若直线xsin α+ycos α+l=0和直线 ![]() 垂直,则角
垂直,则角 ![]() .
.
其中正确命题的序号为 . (把你认为正确的命题序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com