
【题目】设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,
时, ![]() .
.
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() ;
; ![]() 的单调递增区间为
的单调递增区间为![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】【试题分析】(1)直接对函数![]() 求导得
求导得![]() ,借助导函数值的符号与函数单调性之间的关系求出其单调区间;(2)先将不等式
,借助导函数值的符号与函数单调性之间的关系求出其单调区间;(2)先将不等式![]() 中参数分离分离出来可得:
中参数分离分离出来可得: ![]() ,再构造函数
,再构造函数![]() ,
, ![]() ,求导得
,求导得![]() ,借助
,借助![]() ,推得
,推得![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减, ![]() ,进而求得
,进而求得![]() ;(3)先将不等式
;(3)先将不等式![]() 等价转化为
等价转化为![]() ,再构造函数
,再构造函数![]() ,求导可得
,求导可得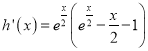 ,由(2)知
,由(2)知![]() 时,
时, ![]() 恒成立,所以
恒成立,所以![]() ,即
,即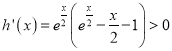 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,因此
,因此![]() 时,有
时,有![]() :
:
解:(1))当![]() 时,则
时,则![]() ,令
,令![]() 得
得![]() ,所以有
,所以有

即![]() 时,
时, ![]() 的单调递减区间为
的单调递减区间为![]() ;
; ![]() 的单调递增区间为
的单调递增区间为![]() .
.
(2)由![]() ,分离参数可得:
,分离参数可得: ![]() ,
,
设![]() ,
, ![]() ,
,
∴![]() ,又∵
,又∵![]() ,
,
∴![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]()
即![]() 的取值范围为
的取值范围为![]() .
.
(3)证明: ![]() 等价于
等价于![]()
设![]() ,
,
∴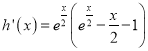 ,由(2)知
,由(2)知![]() 时,
时, ![]() 恒成立,
恒成立,
所以![]() ,
,
∴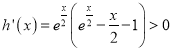 恒成立
恒成立
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,因此
,因此![]() 时,有
时,有![]() .
.


科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),f(0)≠0,f(1)=2,当x>0,f(x)>1,且对任意a,b∈R,有f(a+b)=f(a)f(b).
(1)求证:对任意x∈R,都有f(x)>0;
(2)判断f(x)在R上的单调性,并用定义证明;
(3)求不等式f(3﹣2x)>4的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() )为奇函数,且相邻两对称轴间的距离为
)为奇函数,且相邻两对称轴间的距离为![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递减区间;
的单调递减区间;
(2)将函数![]() 的图象沿
的图象沿![]() 轴方向向右平移
轴方向向右平移![]() 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图象.当
的图象.当![]() 时,求函数
时,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查了50人,并将调查情况进行整理后制成下表:

(1)规定:年龄在![]() 内的为青年人,年龄在
内的为青年人,年龄在![]() 内的为中年人,根据以上统计数据填写下面
内的为中年人,根据以上统计数据填写下面![]() 列联表:
列联表:

(2)能否在犯错误的概率不超过0.025的前提下,认为赞成“车辆限行”与年龄有关?
参考公式和数据:  ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①若![]() ,则“
,则“![]() ”是“
”是“![]() ”成立的充分不必要条件;
”成立的充分不必要条件;
②若椭圆![]() 的两个焦点为
的两个焦点为![]() ,且弦
,且弦![]() 过点
过点![]() ,则
,则![]() 的周长为16;
的周长为16;
③若命题“![]() ”与命题“
”与命题“![]() 或
或![]() ”都是真命题,则命题
”都是真命题,则命题![]() 一定是真命题;
一定是真命题;
④若命题![]() :
: ![]() ,则
,则![]() :
: ![]()
其中为真命题的是__________(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到理科题的概率;
(2)该考生答对理科题的概率均为![]() ,若每题答对得10分,否则得零分,现该生抽到3道理科题,求其所得总分
,若每题答对得10分,否则得零分,现该生抽到3道理科题,求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com