Question

13．如图，等腰梯形ABCD中，AB∥CD，AD⊥BD，矩形ABEF所在的平面和平面ABCD相互垂直． 
（1）求证：AD⊥平面DBE；
（2）若AB=2，AD=AF=1，求三棱锥C-BDE的体积．

Answer 1

分析 （1）要证线与面垂直，需先证明直线AF垂直于平面内的两条相交直线，因为矩形ABCD所在的平面和平面ABEF互相垂直，所以BC垂直于平面ABEF，从而AF垂直于BC，依题意，AF垂直于BF，从而得证．
（2）三棱锥E-BCD与三棱锥C-BDE的体积相等，先计算底面三角形BCD的面积，算三棱锥C-BEF的高，即为BE，最后由三棱锥体积计算公式计算即可．

解答 （1）证明：∵平面ABCD⊥平面ABEF．
平面ABCD∩平面ABEF=AB．
∵矩形ABEF．
∴EB⊥AB．∵EB?平面ABEF．
∴EB⊥平面ABCD                                           （3分）
∵AD?平面ABCD．
∵EB⊥AD，AD⊥BD，BD∩EB=B．
∴AD⊥平面BDE                                            （6分）
（2）∵AD=1，AD⊥BD，AB=2，
∴∠DAB=60°，过点C作CH⊥AB于H，则∠CBH=60°，
∴CH=$\frac{{\sqrt{3}}}{2}$，CD=AB-2HB=1，（9分）
故S_△BCD=$\frac{1}{2}$×1×$\frac{{\sqrt{3}}}{2}$=$\frac{{\sqrt{3}}}{4}$，∵EB⊥平面ABCD，
∴三棱锥E-BCD的高为EB=1，∴V_E-BCD=$\frac{1}{3}$×S_△BCD×BE=$\frac{1}{3}$×$\frac{{\sqrt{3}}}{4}$×1=$\frac{{\sqrt{3}}}{12}$（12分）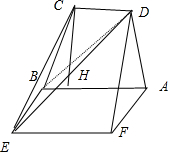

点评 本题考查了线面平行的判定，即等体积法求三棱锥的体积，属于基础题．