
分析 (1)分别令x=1,x=-1,代入已知的等式,化简变形可得(a0+a2+a4+…+a50)2-(a1+a3+a5+…+a49)2的值.
(2)由条件利用(1+$\sqrt{x}{)^n}$的展开式的通项公式,可得$C_n^8+C_n^{10}=2C_n^9$,计算求得n的值.
解答 解:(1)令x=1,得${(2-\sqrt{3})^{50}}={a_0}+{a_1}+{a_2}+…+{a_{50}};①$,
令x=-1,得${(2+\sqrt{3})^{50}}={a_0}-{a_1}+{a_2}-…+{a_{50}};②$,
把①②相乘得(a0+a1+a2+a3+a4+…+a50)=(a0-a1+a2 -a3+a4+…-a49+a50)
=(a0+a2+a4+…+a50)2-(a1+a3+a5+…+a49)2 =150=1.
(2)由于(1+$\sqrt{x}{)^n}$的展开式的通项公式为 ${T_{r+1}}=C_n^r{x^{\frac{r}{2}}}$,由题知$C_n^8+C_n^{10}=2C_n^9$,
即 $\frac{n!}{8!(n-8)!}$+$\frac{n!}{10!(n-10)!}$=2•$\frac{n!}{9!(n-9)!}$,化简可的n2-37n+322=0,求得n=14,或 n=23.
点评 本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案;还考查了二项展开式的通项公式,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | a3>b3 | B. | $\frac{1}{a}$<$\frac{1}{b}$ | C. | lga>lgb | D. | $\sqrt{a}$>$\sqrt{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{{6\sqrt{13}}}{13}$ | C. | $\frac{{4\sqrt{13}}}{13}$ | D. | $\frac{{2\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有1名男生和至少有1名女生 | B. | 恰有1名男生和恰有2名男生 | ||
| C. | 至少有1名男生和都是女生 | D. | 至多有1名男生和都是女生 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
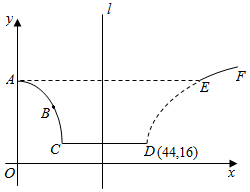 在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$
在股票市场上,投资者常参考股价(每一股的价格)的某条平滑均线的变化情况来决定买入或卖出股票.股民老张在研究股票的走势图时,发现一只股票的均线近期走得很有特点:如果按如图所示的方式建立平面直角坐标系xOy,则股价y(元)和时间x的关系在ABC段可近似地用解析式y=asin(ωx+φ)+b(0<φ<π)来描述,从C点走到今天的D点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且D点和C点正好关于直线l:x=34对称.老张预计这只股票未来的走势如图中虚线所示,这里DE段与ABC段关于直线l对称,EF段是股价延续DE段的趋势(规律)走到这波上升行情的最高点F.现在老张决定取点A(0,22),点B(12,19),点D(44,16)来确定解析式中的常数a,b,ω,φ,并且求得ω=$\frac{π}{72}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x<log2x<${({\frac{1}{2}})^x}$ | B. | 2x<${({\frac{1}{2}})^x}$<log2x | C. | ${({\frac{1}{2}})^x}$<log2x<2x | D. | log2x<${({\frac{1}{2}})^x}$<2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com