
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为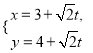 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系
轴的正半轴为极轴建立极坐标系,并使得它与直角坐标系![]() 有相同的长度单位,曲线
有相同的长度单位,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() 点的坐标为
点的坐标为![]() ,求
,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 且与
且与![]() 轴垂直的弦长为3.
轴垂直的弦长为3.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 作直线
作直线![]() 与椭圆交于
与椭圆交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值,若存在,请求出
为定值,若存在,请求出![]() 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知极坐标系的极点在直角坐标系的原点处,极轴与![]() 轴的非负半轴重合,直线
轴的非负半轴重合,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设![]() ,
, ![]() 分别是直线
分别是直线![]() 与曲线
与曲线![]() 上的点,求
上的点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() ,
,![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设该椭圆![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() (点
(点![]() 位于点
位于点![]() 的上方),直线
的上方),直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 的交点
的交点![]() 在定直线上.
在定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市县乡教师流失现象非常严重,为了县乡孩子们能接受良好教育,某市今年要为两所县乡中学招聘储备未来三年的教师,已知现在该市县乡中学无多余教师,为决策应招聘多少县乡教师搜集并整理了该市50所县乡中学在过去三年内的教师流失数,得到如表的频率分布表:以这50所县乡中学流失教师数的频率代替一所县乡中学流失教师数发生的概率.
(1)求该市所有县乡中学教师流失数不低于8的概率;
(2)若从上述50所县乡中学中流失教师数不低于9的县乡学校中任取两所调查回访,了解其中原因,求这两所学校的教师流失数都是10的概率.
流失教师数 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 2 | 4 | 11 | 16 | 12 | 3 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com