
 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.
 与
与 之间的函数关系式
之间的函数关系式 ;
; 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据:
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据: ).
). 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源:不详 题型:填空题
 吨,每次都购买
吨,每次都购买 吨,运费为
吨,运费为 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为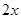 万元,若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.
万元,若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com