
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,0) | C. | (-∞,e) | D. | (-∞,1) |
分析 若?x0∈(0,+∞),不等式ax-lnx<0成立,则?x0∈(0,+∞),不等式a<$\frac{lnx}{x}$成立,令f(x)=$\frac{lnx}{x}$,则a<f(x)max,利用导数法,求出函数的最大值,可得答案.
解答 解:若?x0∈(0,+∞),不等式ax-lnx<0成立,
则?x0∈(0,+∞),不等式a<$\frac{lnx}{x}$成立,
令f(x)=$\frac{lnx}{x}$,则a<f(x)max,
∵f′(x)=$\frac{1-lnx}{{x}^{2}}$,
则x∈(0,e)时,f′(x)>0,f(x)=$\frac{lnx}{x}$为增函数,
x∈(e,+∞)时,f′(x)<0,f(x)=$\frac{lnx}{x}$为减函数,
故x=e时,f(x)max=$\frac{1}{e}$,
故a的取值范围是(-∞,$\frac{1}{e}$).
故选:A.
点评 本题考查了存在性问题,注意运用参数分离,利用导数求函数的最值是解题的关键,考查运算能力,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$≤k≤2 | B. | k≤-$\frac{1}{2}$或k≥2 | C. | -2≤k≤$\frac{1}{2}$ | D. | k≤-2或k≥$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
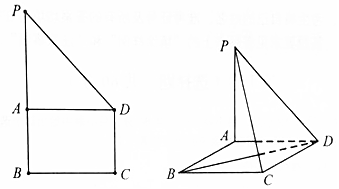 如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.
如图,在直角梯形PBCD中,PB∥DC,DC⊥BC,点A在边PB上,AD∥BC,PB=3BC=6,现沿AD将△PAD折起,使平面PAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果α⊥β,那么α内一定存在直线平行于β | |
| B. | 如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ | |
| C. | 如果α不垂直于β,那么α内一定不存在直线垂直于β | |
| D. | 如果α⊥β,那么α内所有直线都垂直于β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-2x-1≥0 | B. | ?x∈R,x2-2x-1<0 | C. | ?x∈R,x2-2x-1<0 | D. | ?x∈R,x2-2x-1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
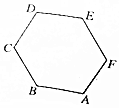
| A. | $\overrightarrow{EB}$ | B. | $\overrightarrow{BE}$ | C. | $\overrightarrow{AD}$ | D. | $\overrightarrow{CF}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com