【题目】某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李，小王设计的底座形状分别为
， 
，经测量
米， 
米， 
米， 
（I）求
的长度；
（Ⅱ）若环境标志的底座每平方米造价为
元，不考虑其他因素，小李，小王谁的设计建造费用最低（请说明理由），最低造价为多少？（
）
科目：高中数学 来源： 题型：
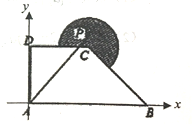
【题目】如图，在直角坐标系xoy中，其中A(0,0),B(2,0),C(1,1),D(0,1),图中圆弧所在圆的圆心为点C，半径为
，且点P在图中阴影部分（包括边界）运动.若
，其中
，则
的取值范围是（ ）
A. [2,3+
] B. [2,3+
] C. [3-
, 3+
] D. [3-
, 3+
]
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为对南康区和于都县两区县某次联考成绩进行分析，随机抽查了两地一共10000名考生的成绩，根据所得数据画了如下的样本频率分布直方图．
(1)求成绩在
的频率；
(2)根据频率分布直方图算出样本数据平均数；
(3)为了分析成绩与班级、学校等方面的关系，必须按成绩再从这10000人中用分层抽样方法抽出20人作进一步分析，则成绩在
的这段应抽多少人？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
： 
的焦点为
，准线为
，三个点
， 
， 
中恰有两个点在
上．
（1）求抛物线
的标准方程；
（2）过
的直线交
于
， 
两点，点
为
上任意一点，证明：直线
， 
， 
的斜率成等差数列．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知圆C与y轴相切于点T(0,2)，与x轴的正半轴交于两点
(点
在点
的左侧)，且
.
(1)求圆C的方程；(2)过点
任作一直线与圆O： 
相交于
两点，连接
，求证： 
定值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,
(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解某地区某种农产品的年产量
（单位：吨）对价格
（单位：千元/吨）和利润
的影响，对近五年该农产品的年产量和价格统计如下表：
| 1 | 2 | 3 | 4 | 5 |
| 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
已知
和
具有线性相关关系.
（Ⅰ）求
关于
的线性回归方程
；
（Ⅱ）若每吨该农产品的成本为2千元，假设该农产品可全部卖出，预测当年产量为多少吨时，年利润
取到最大值？（保留一位小数）
参考数据及公式： 
， 
，
， 
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆
的离心率为
，且过点
.
（1）求椭圆
的方程；
（2）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆
恒有两个交点
， 且
（
为坐标原点）？若存在，写出该圆的方程；若不存在，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
