
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数![]() 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(2)设![]() ,若函数
,若函数![]() 对任意
对任意![]() 都成立,求
都成立,求![]() 的最大值.
的最大值.
【答案】(1) 当![]() 时,增区间为
时,增区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)通过函数![]() ,得
,得![]() ,然后结合
,然后结合![]() 与0的关系对a的正负进行讨论即可;(2)对a的正负进行讨论:当a<0时,
与0的关系对a的正负进行讨论即可;(2)对a的正负进行讨论:当a<0时, ![]() 不可能恒成立;当a=0时,此时ab=0;当a>0时,由题结合(1)得
不可能恒成立;当a=0时,此时ab=0;当a>0时,由题结合(1)得![]() ,设
,设![]() ,问题转化为求
,问题转化为求![]() 的最大值,利用导函数即可.
的最大值,利用导函数即可.
试题解析::(1)由函数![]() ,可知
,可知![]() ,
,
![]() 时,
时, ![]() ,函数
,函数![]() 在R上单调递增;
在R上单调递增;
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
故当![]() 时,
时, ![]() ,此时
,此时![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增.
单调递增.
综上所述,当![]() 时,函数
时,函数![]() 在单调递增区间为
在单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
(2)由(1)知,当![]() 时,函数
时,函数![]() 在R上单调递增且当
在R上单调递增且当![]() 时,
时, ![]() 不可能恒成立;
不可能恒成立;
当a=0时,此时ab=0;
当a>0时,由函数![]() 对任意x∈R都成立,可得
对任意x∈R都成立,可得![]() ,
,
∵![]() ,
,
设![]() ,则
,则![]() ,
,
由于![]() ,令
,令![]() ,得
,得![]()
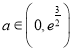 时,
时, ![]() 单调递增;
单调递增;
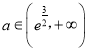 时,
时, ![]() 单调递减.
单调递减.
![]() ,即当
,即当![]() 时,ab的最大值为
时,ab的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知坐标平面上动点![]() 与两个定点
与两个定点![]() ,
, ![]() ,且
,且![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段长度为8,求直线
所截得的线段长度为8,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式.
)的函数解析式.
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
![]()
以100天记录的各需求量的频率作为各需求量发生的概率.
(1)若花店一天购进17枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)若花店计划一天购进16枝或17枝玫瑰花,以利润角度看,你认为应购进16枝好还是17枝好?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体![]() 中,四边形
中,四边形![]() 为矩形,四边形
为矩形,四边形![]() 为梯形,
为梯形, ![]() ,平面
,平面![]() 与平面
与平面![]() 垂直,且
垂直,且![]() .
.
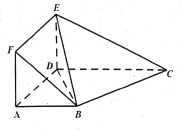
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() ,且平面
,且平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】无穷数列![]() 满足:
满足: ![]() 为正整数,且对任意正整数
为正整数,且对任意正整数![]() ,
, ![]() 为前
为前![]() 项
项![]() ,
, ![]() ,
, ![]() ,
, ![]() 中等于
中等于![]() 的项的个数.
的项的个数.
(Ⅰ)若![]() ,请写出数列
,请写出数列![]() 的前7项;
的前7项;
(Ⅱ)求证:对于任意正整数![]() ,必存在
,必存在![]() ,使得
,使得![]() ;
;
(Ⅲ)求证:“![]() ”是“存在
”是“存在![]() ,当
,当![]() 时,恒有
时,恒有![]()
![]() 成立”的充要条件。
成立”的充要条件。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N的距离的![]() 倍.
倍.
(1)求曲线E的方程;
(2)已知m≠0,设直线![]() :x﹣my﹣1=0交曲线E于A,C两点,直线
:x﹣my﹣1=0交曲线E于A,C两点,直线![]() :mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
:mx+y﹣m=0交曲线E于B,D两点,若CD的斜率为﹣1时,求直线CD的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com