
 ,求AC的长.
,求AC的长.
 (本小题满分14分)
(本小题满分14分) ,
, .…(5分)
.…(5分) ,所以
,所以 .…(6分)
.…(6分) .…(7分)
.…(7分) ,
,
 =
= .…(8分)
.…(8分) ,
, .…(9分)
.…(9分) .…(10分)
.…(10分) .…(11分)
.…(11分) 在Rt△AOH中,因为
在Rt△AOH中,因为 ,
, =
= .…(12分)
.…(12分) ,
, .…(13分)
.…(13分) .
. 或
或 .…(14分)
.…(14分)

科目:高中数学 来源: 题型:
 如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 3 |

查看答案和解析>>
科目:高中数学 来源: 题型:
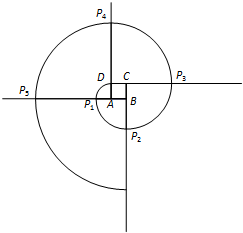 (2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是
(2011•丰台区二模)如图所示,已知正方形ABCD的边长为1,以A为圆心,AD长为半径画弧,交BA的延长线于P1,然后以B为圆心,BP1长为半径画弧,交CB的延长线于P2,再以C为圆心,CP2长为半径画弧,交DC的延长线于P3,再以D为圆心,DP3长为半径画弧,交AD的延长线于P4,再以A为圆心,AP4长为半径画弧,…,如此继续下去,画出的第8道弧的半径是| n(n+1)π |
| 4 |
| n(n+1)π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
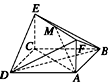
求证:
(1)AM∥平面BDE;
(2)AM⊥平面BDF.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省哈尔滨市高二下期中考试文数学卷(解析版) 题型:解答题
如图所示,已知正方形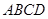 和矩形
和矩形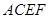 所在的平面互相垂直,
所在的平面互相垂直,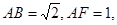
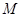 是线段
是线段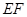 的中点。
的中点。
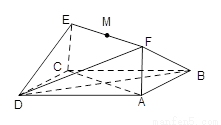
(1)证明: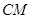 ∥平面
∥平面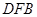
(2)求异面直线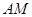 与
与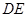 所成的角的余弦值。
所成的角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com