
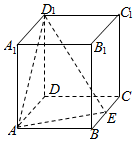
 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F∥平面AD1E,则直线A1F与平面BCC1B1所成的角的正切值t构成的集合是( )
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F∥平面AD1E,则直线A1F与平面BCC1B1所成的角的正切值t构成的集合是( )| A. | {t|${\frac{{2\sqrt{5}}}{5}$≤t≤$\frac{{2\sqrt{3}}}{3}}\right.}$} | B. | {t|{2≤t≤2$\sqrt{3}}$} | C. | {t|${\frac{{2\sqrt{5}}}{5}$≤t≤2$\sqrt{3}$} | D. | {{t|{2≤t≤2$\sqrt{2}}$} |
分析 设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点.分别取B1B、B1C1的中点M、N,连接AM、MN、AN,可证出平面A1MN∥平面D1AE,从而得到A1F是平面A1MN内的直线.由此将点F在线段MN上运动并加以观察,即可得到A1F与平面BCC1B1所成角取最大值、最小值的位置,由此不难得到A1F与平面BCC1B1所成角的正切取值范围.
解答 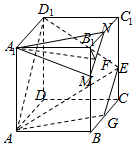 解:设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
解:设平面AD1E与直线BC交于点G,连接AG、EG,则G为BC的中点
分别取B1B、B1C1的中点M、N,连接AM、MN、AN,则
∵A1M∥D1E,A1M?平面D1AE,D1E?平面D1AE,
∴A1M∥平面D1AE.同理可得MN∥平面D1AE,
∵A1M、MN是平面A1MN内的相交直线
∴平面A1MN∥平面D1AE,
由此结合A1F∥平面D1AE,可得直线A1F?平面A1MN,即点F是线段MN上上的动点.
设直线A1F与平面BCC1B1所成角为θ
运动点F并加以观察,可得
当F与M(或N)重合时,A1F与平面BCC1B1所成角等于∠A1MB1,此时所成角θ达到最小值,满足tanθ=$\frac{{A}_{1}{B}_{1}}{{B}_{1}M}$=2;
当F与MN中点重合时,A1F与平面BCC1B1所成角达到最大值,满足tanθ=$\frac{{A}_{1}{B}_{1}}{\frac{\sqrt{2}}{2}{B}_{1}M}$=2$\sqrt{2}$
∴A1F与平面BCC1B1所成角的正切取值范围为[2,2$\sqrt{2}$].
故选:D.
点评 本题给出正方体中侧面BCC1B1内动点F满足A1F∥平面D1AE,求A1F与平面BCC1B1所成角的正切取值范围,着重考查了正方体的性质、直线与平面所成角、空间面面平行与线面平行的位置关系判定等知识,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ac>bc | B. | ac2≥bc2 | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | $\frac{a}{b}$>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
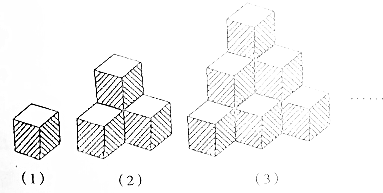 如图是由一些小正方体摞成的,第(1)堆有1个,第(2)堆有4个,第(3)堆有10个…,则第n堆有$\frac{n(n+1)(n+2)}{6}$小正方体.
如图是由一些小正方体摞成的,第(1)堆有1个,第(2)堆有4个,第(3)堆有10个…,则第n堆有$\frac{n(n+1)(n+2)}{6}$小正方体.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com