
【题目】已知函数f(x)= ![]() .
.
(1)当 ![]() 时,求函数f(x)的取值范围;
时,求函数f(x)的取值范围;
(2)将f(x)的图象向左平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间.
个单位得到函数g(x)的图象,求g(x)的单调递增区间.
【答案】
(1)解:∵f(x)= ![]() =
= ![]() =sin(2x﹣
=sin(2x﹣ ![]() ),
),
∵ ![]() 时,2x﹣
时,2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
∴sin(2x﹣ ![]() )∈[﹣
)∈[﹣ ![]() ,1].
,1].
∴函数f(x)的取值范围为:[﹣ ![]() ,1]
,1]
(2)解:∵g(x)=f(x+ ![]() )=sin[2(x+
)=sin[2(x+ ![]() )﹣
)﹣ ![]() ]=sin(2x+
]=sin(2x+ ![]() ),
),
∴令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可解得g(x)的单调递增区间为:[k
,k∈Z,即可解得g(x)的单调递增区间为:[k ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
【解析】(1)利用三角函数恒等变换的应用化简可求f(x)=sin(2x﹣ ![]() ),由
),由 ![]() ,可求2x﹣
,可求2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],根据正弦函数的图象和性质可求f(x)的取值范围.(2)根据函数y=Asin(ωx+φ)的图象变换可求g(x)=f(x+
],根据正弦函数的图象和性质可求f(x)的取值范围.(2)根据函数y=Asin(ωx+φ)的图象变换可求g(x)=f(x+ ![]() )=sin(2x+
)=sin(2x+ ![]() ),令2kπ﹣
),令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,即可解得g(x)的单调递增区间.
,k∈Z,即可解得g(x)的单调递增区间.
【考点精析】利用函数y=Asin(ωx+φ)的图象变换对题目进行判断即可得到答案,需要熟知图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.


科目:高中数学 来源: 题型:
【题目】已知圆心为C的圆经过O(0,0))和A(4,0)两点,线段OA的垂直平分线和圆C交于M,N两点,且|MN|=2 ![]()
(1)求圆C的方程
(2)设点P在圆C上,试问使△POA的面积等于2的点P共有几个?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[0,1]上的函数f(x)满足:①f(0)=0;②f(x)+f(1﹣x)=1;③f( ![]() )=
)= ![]() f(x);④当0≤x1<x2≤1时,f(x1)≤f(x2).则f(
f(x);④当0≤x1<x2≤1时,f(x1)≤f(x2).则f( ![]() )= .
)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
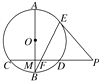
【题目】如图,已知⊙O中,直径AB垂直于弦CD,垂足为M,P是CD延长线上一点,PE切⊙O于点E,连接BE交CD于点F,证明:
(1)∠BFM=∠PEF;
(2)PF2=PD·PC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个图形F1 , F2 , 我们将图象F1上任意一点与图形F2上的任意一点间的距离中的最小值,叫作图形F1与F2图形的距离,若两个函数图象的距离小于1,则这两个函数互为“可及函数”,给出下列几对函数,其中互为“可及函数”的是 . (写出所有正确命题的编号) ①f(x)=cosx,g(x)=2;
②f(x)=ex . g(x)=x;
③f(x)=log2(x2﹣2x+5),g(x)=sin ![]() ﹣x;
﹣x;
④f(x)=x+ ![]() ,g(x)=lnx+2.
,g(x)=lnx+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2﹣xlna(a>0且a≠1)
(1)求函数f(x)单调递增区间;
(2)若存在x1 , x2∈[﹣1,1],使得|f(x1)﹣f(x2)|≥e﹣1(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A( ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ). (Ⅰ)求
). (Ⅰ)求 ![]() ,
, ![]() 夹角的余弦值;
夹角的余弦值;
(Ⅱ)已知C(1,0),记∠AOC=α,∠BOC=β,求tan ![]() 的值.
的值.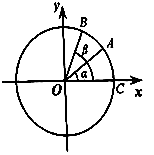
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布图如图所示,下表是年龄的频率分布表.
,得到的频率分布图如图所示,下表是年龄的频率分布表.
![]()

(1)现要从年龄较小的第![]() 组中用分层抽样的方法抽取6人,则年龄第
组中用分层抽样的方法抽取6人,则年龄第![]() 组人数分别是多少?
组人数分别是多少?
(2)在(1)的条件下,从这6中随机抽取2参加社区宣传交流活动,X表示第3组中抽取的人数,求X的分布列和期望值
查看答案和解析>>
科目:高中数学 来源: 题型:
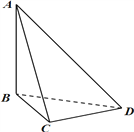
【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,则三棱锥
,则三棱锥![]() 的外接球的球面面积为__________.
的外接球的球面面积为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com