
|
| 1 |
| x |
| 1 |
| x |
|
|
|
 ,
,| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |


科目:高中数学 来源: 题型:
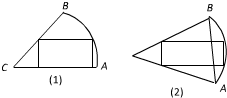 某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.
某工厂生产主要产品后,留下大量中心角为60°,半径为a的扇形边角料,现要废物利用,从中剪裁出矩形毛坯,要求矩形面积尽可能大,并如图设计了两种裁剪方法,一种是使矩形的一边落在扇形的半径上,另一种是使矩形的两顶点分别在扇形的两条半径上,请选出最佳方案.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com