
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为![]() .
.
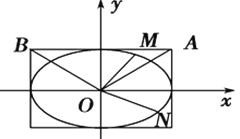
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)不过原点![]() 的直线与椭圆
的直线与椭圆![]() 交于两点
交于两点![]() 、
、![]() ,且直线
,且直线![]() 、
、![]() 、
、![]() 的斜率依次成等比数列,问:直线是否定向的,请说明理由.
的斜率依次成等比数列,问:直线是否定向的,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图和90后从事互联网行业者岗位分布图(90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生),则下列结论中不一定正确的是( )
整个互联网行业从业者年龄分布饼状图 90后从事互联网行业者岗位分布图
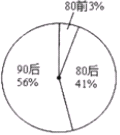
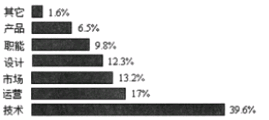
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数90后比80后多
C.互联网行业中从事设计岗位的人数90后比80前多
D.互联网行业中从事市场岗位的90后人数不足总人数的10%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,直线l经过
,直线l经过![]() 与椭圆交于P,Q两点.当
与椭圆交于P,Q两点.当![]() 与y轴的交点是线段
与y轴的交点是线段![]() 的中点时,
的中点时,![]() .
.
(1)求椭圆的方程;
(2)设直线l不垂直于x轴,若![]() 满足
满足![]() ,求t的取值范围.
,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如题所示:扇形ABC是一块半径为2千米,圆心角为60°的风景区,P点在弧BC上,现欲在风景区中规划三条三条商业街道PQ、QR、RP,要求街道PQ与AB垂直,街道PR与AC垂直,直线PQ表示第三条街道。
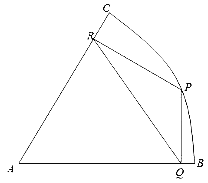
(1)如果P位于弧BC的中点,求三条街道的总长度;
(2)由于环境的原因,三条街道PQ、PR、QR每年能产生的经济效益分别为每千米300万元、200万元及400万元,问:这三条街道每年能产生的经济总效益最高为多少?(精确到1万元)
查看答案和解析>>
科目:高中数学 来源: 题型:
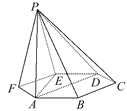
【题目】如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有____________(把所有正确的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】符合以下性质的函数称为“![]() 函数”:①定义域为
函数”:①定义域为![]() ,②
,②![]() 是奇函数,③
是奇函数,③![]() (常数
(常数![]() ),④
),④![]() 在
在![]() 上单调递增,⑤对任意一个小于
上单调递增,⑤对任意一个小于![]() 的正数
的正数![]() ,至少存在一个自变量
,至少存在一个自变量![]() ,使
,使![]() .下列四个函数中
.下列四个函数中![]() ,
,![]() ,
, ,
, 中“
中“![]() 函数”的个数为( )
函数”的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
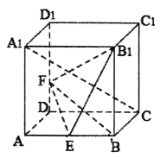
【题目】如图,正方体![]() 中,E为AB中点,F在线段
中,E为AB中点,F在线段![]() 上.给出下列判断:①存在点F使得
上.给出下列判断:①存在点F使得![]() 平面
平面![]() ;②在平面
;②在平面![]() 内总存在与平面
内总存在与平面![]() 平行的直线;③平面
平行的直线;③平面![]() 与平面ABCD所成的二面角(锐角)的大小与点F的位置无关;④三棱锥
与平面ABCD所成的二面角(锐角)的大小与点F的位置无关;④三棱锥![]() 的体积与点F的位置无关.其中正确判断的有( )
的体积与点F的位置无关.其中正确判断的有( )
A.①②B.③④C.①③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com