
【题目】众所周知,城市公交车的数量太多会造成资源的浪费,太少又难以满足乘客的需求,为此,某市公交公司在某站台的50名候车乘客中随机抽取10名,统计了他们的候车时间(单位:分钟),得到下表.
候车时间 | 人数 |
| 1 |
| 4 |
| 2 |
| 2 |
| 1 |
(1)估计这10名乘客的平均候车时间(同一组中的每个数据可用该组区间的中点值代替);
(2)估计这50名乘客的候车时间少于10分钟的人数.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】2019年的天猫“双11”交易金额又创新高,达到2684亿元,物流爆增.某机构为了了解网购者对收到快递的满意度进行调查,对某市5000名网购者发出满意度调查评分表,收集并随机抽取了200名网购者的调查评分(评分在70~100分之间),其频率分布直方图如图,评分在95分及以上确定为“非常满意”.
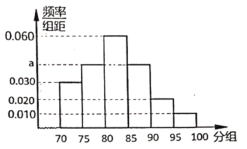
(1)求![]() 的值;
的值;
(2)以样本的频率作概率,试估计本次调查的网购者中“非常满意”的人数;
(3)按分层抽样的方法,从评分在90分及以上的网购者中抽取6人,再从这6人中随机地选取2人,求至少选到一个“非常满意”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月25日,第![]() 届罗马尼亚数学大师赛(简称
届罗马尼亚数学大师赛(简称![]() )于罗马尼亚首都布加勒斯特闭幕,最终成绩揭晓,以色列选手排名第一,而中国队无一人获得金牌,最好成绩是获得银牌的第
)于罗马尼亚首都布加勒斯特闭幕,最终成绩揭晓,以色列选手排名第一,而中国队无一人获得金牌,最好成绩是获得银牌的第![]() 名,总成绩排名第
名,总成绩排名第![]() .而在分量极重的国际数学奥林匹克(
.而在分量极重的国际数学奥林匹克(![]() )比赛中,过去拿冠军拿到手软的中国队,也已经有连续
)比赛中,过去拿冠军拿到手软的中国队,也已经有连续![]() 年没有拿到冠军了.人们不禁要问“中国奥数究竟怎么了?”,一时间关于各级教育主管部门是否应该下达“禁奥令”成为社会热点.某重点高中培优班共
年没有拿到冠军了.人们不禁要问“中国奥数究竟怎么了?”,一时间关于各级教育主管部门是否应该下达“禁奥令”成为社会热点.某重点高中培优班共![]() 人,现就这
人,现就这![]() 人“禁奥令”的态度进行问卷调查,得到如下的列联表:
人“禁奥令”的态度进行问卷调查,得到如下的列联表:
不应下“禁奥令” | 应下“禁奥令” | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
若采用分层抽样的方法从![]() 人中抽出
人中抽出![]() 人进行重点调查,知道其中认为不应下“禁奥令”的同学共有
人进行重点调查,知道其中认为不应下“禁奥令”的同学共有![]() 人.
人.
(1)请将上面的列联表补充完整,并判断是否有![]() 的把握认为对下“禁奥令”的态度与性别有关?请说明你的理由;
的把握认为对下“禁奥令”的态度与性别有关?请说明你的理由;
(2)现从这![]() 人中抽出
人中抽出![]() 名男生、
名男生、![]() 名女生,记此
名女生,记此![]() 人中认为不应下“禁奥令”的人数为
人中认为不应下“禁奥令”的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式与数据:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园举办“yue”主题系列活动——“悦”动越健康亲子运动打卡活动,为了解小朋友坚持打卡的情况,对该幼儿园所有小朋友进行了调查,调查结果如下表:
打卡天数 | 17 | 18 | 19 | 20 | 21 |
男生人数 | 3 | 5 | 3 | 7 | 2 |
女生人数 | 3 | 5 | 5 | 7 | 3 |
(1)根据上表数据,求该幼儿园男生平均打卡的天数;
(2)若从打卡21天的小朋友中任选2人交流心得,求选到男生和女生各1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体ABCD-A1B1C1D1 的棱长为 2,且AC 与BD 交于点O,E 为棱DD1 中点,以A 为原点,建立空间直角坐标系A-xyz,如图所示.
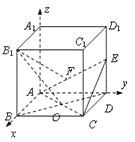
(Ⅰ)求证:B1O⊥平面EAC;
(Ⅱ)若点F 在EA 上且B1F⊥AE,试求点F 的坐标;
(Ⅲ)求二面角B1-EA-C 的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是古代中国劳动人民发明的一种中国传统智力玩具,它由五块等腰直角三角形,一块正方形和一块平行四边形共七块板组成.清陆以湉《冷庐杂识》卷一中写道:近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.如图是一个用七巧板拼成的正方形,若在此正方形中任取一点,则此点取自阴影部分的概率为( )
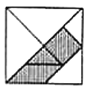
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com