
【题目】如图,在四棱锥![]() 中,平面
中,平面![]()
![]() 平面
平面![]() ,BC//平面PAD,
,BC//平面PAD, ![]()
![]() ,
,![]() .
.
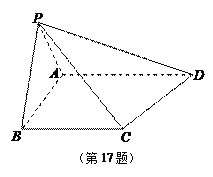
求证:(1) ![]() 平面
平面![]() ;
;
(2)平面![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)由BC//平面PAD可得BC//AD,根据线面平行的判定定理可得![]() 平面
平面![]() ;(2)过P作PH
;(2)过P作PH ![]() AB于H,由条件可得
AB于H,由条件可得![]() 平面
平面![]() ,从而可证得BC
,从而可证得BC ![]() PH,又BC
PH,又BC ![]() PB,故有BC
PB,故有BC ![]() 平面PAB,所以平面PBC
平面PAB,所以平面PBC ![]() 平面PAB .
平面PAB .
试题解析:
(1)因为BC//平面PAD,
而BC![]() 平面ABCD,平面ABCD
平面ABCD,平面ABCD![]() 平面PAD = AD,
平面PAD = AD,
所以BC//AD ,
又因为AD ![]() 平面PBC,BC
平面PBC,BC![]() 平面PBC,
平面PBC,
所以![]() 平面
平面![]()

(2)过P作PH ![]() AB于H,
AB于H,
因为平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]() =AB,
=AB,
所以![]() 平面
平面![]()
因为BC ![]() 平面ABCD,
平面ABCD,
所以BC ![]() PH.
PH.
因为![]()
![]() ,
,
所以BC ![]() PB,
PB,
而![]() ,
,
于是点H与B不重合,即PB ![]() PH = H.
PH = H.
因为PB,PH ![]() 平面PAB,
平面PAB,
所以BC ![]() 平面PAB
平面PAB
因为BC ![]() 平面PBC,
平面PBC,
故平面PBC ![]() 平面
平面![]() AB.
AB.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +b,其中a,b是常数且a>0.
+b,其中a,b是常数且a>0.
(1)用函数单调性的定义证明f(x)在区间(0, ![]() ]上是单调递减函数;
]上是单调递减函数;
(2)已知函数f(x)在区间[ ![]() ,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
,+∞)上是单调递增函数,且在区间[1,2]上f(x)的最大值为5,最小值为3,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 在
在![]() 的单调区间;
的单调区间;
(Ⅱ)方程![]() 有3个不同的实根,求实数
有3个不同的实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,若对于任意的
时,若对于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求满足条件的正整数
,求满足条件的正整数![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
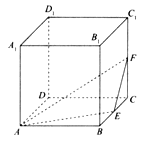
【题目】(文科选做)如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E、F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段A1P长度的取值范围是_____。
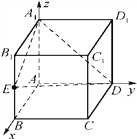
(理科选做)在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos4x﹣sin4x.下列结论正确的是( )
A.函数f(x)在区间[0, ![]() ]上是减函数
]上是减函数
B.函数f(x)的图象关于原点对称
C.f(x)的最小正周期为 ![]()
D.f(x)的值域为[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔优秀学生参加广州市高二级数学竞赛.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取了5次,记录如下(单位:分):
甲 83 81 79 95 92
乙 92 85 75 88 90
(1)甲乙两人分数的极差分别是多少?并用茎叶图表示这两组数据.
(2)甲乙两人这5次成绩的平均分和方差各是多少?从稳定性的角度考虑,你认为选派哪位学生参加比赛较合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com