
【题目】如图1,等腰梯形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起后如图2,使二面角
折起后如图2,使二面角![]() 成直二面角,设
成直二面角,设![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 的中
的中
点.
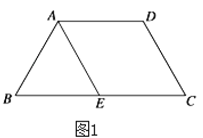

(1)求证:![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)判断![]() 能否垂直于平面
能否垂直于平面![]() ,并说明理由.
,并说明理由.
【答案】(1)答案见解析.(2)答案见解析(3)![]() 与平面
与平面![]() 不垂直,理由见解析
不垂直,理由见解析
【解析】
(1)证明![]() ,只需证明
,只需证明![]() 平面
平面![]() ,利用
,利用![]() 与
与![]() E是等边三角形,即可证明;
E是等边三角形,即可证明;
(2)证明平面![]() 平面
平面![]() ,只需证明
,只需证明![]() 平面
平面![]() ,只需证明
,只需证明![]() 平面
平面![]() 即可;
即可;
(3)![]() 与平面
与平面![]() 不垂直.假设
不垂直.假设![]() 平面
平面![]() ,则
,则![]() ,从而可证明
,从而可证明![]() 平面
平面![]() ,可得
,可得![]() ,这与
,这与![]() 矛盾.
矛盾.
(1)证明:设![]() 中点为
中点为![]() ,连接
,连接![]() ,
,
∵在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,∴
的中点,∴![]() 与
与![]() 都是等边三角形.
都是等边三角形.
∴![]() ,
,![]() .
.
∵![]() ,
,![]()
![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)证明:连接![]() 交
交![]() 于点
于点![]() ,∵
,∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() 是线段
是线段![]() 的中点.
的中点.
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(3)解:![]() 与平面
与平面![]() 不垂直.
不垂直.
证明:假设![]() 平面
平面![]() ,则
,则![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ,这与
,这与![]() 矛盾.
矛盾.
∴![]() 与平面
与平面![]() 不垂直.
不垂直.



 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
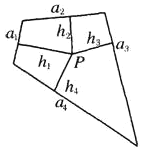
【题目】如图所示,面积为![]() 的平面凸四边形的第
的平面凸四边形的第![]() 条边的边长记为
条边的边长记为![]() ,此四边形内任一点
,此四边形内任一点![]() 到第
到第![]() 条边的距离记为
条边的距离记为![]() ,若
,若![]() ,则
,则![]() .类比以上性质,体积为
.类比以上性质,体积为![]() 的三棱锥的第
的三棱锥的第![]() 个面的面积记为
个面的面积记为![]() ,此三棱锥内任一点
,此三棱锥内任一点![]() 到第
到第![]() 个面的距离记为
个面的距离记为![]() ,若
,若![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2-5x+b>0的解是-3<x<2,设A={x|bx2-5x+a>0},B={x|![]() }.
}.
(1)求a,b的值;
(2)求A∩B和A∪(UB).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(单位:辆)与创造的价值y(单位:元)之间有如下的关系:![]() .若这家工厂希望在一个星期内利用这条流水线创收60000元以上,则在一个星期内大约应该生产多少辆摩托车?
.若这家工厂希望在一个星期内利用这条流水线创收60000元以上,则在一个星期内大约应该生产多少辆摩托车?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCDEF中,四边形ABCD为矩形,二面角A-CD-F为60°,DE∥CF,CD⊥DE,AD=2,DE=DC=3,CF=6.

(1)求证:BF∥平面ADE;
(2)在线段CF上求一点G,使锐二面角B-EG-D的余弦值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() .
.
(1)若![]() 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6),先后抛掷两次时第一次、第二次出现的点数,求满足
分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6),先后抛掷两次时第一次、第二次出现的点数,求满足![]() 的概率;
的概率;
(2)若![]() 在连续区间
在连续区间![]() 上取值,求满足
上取值,求满足![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com