
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,![]() φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0
φ<0)的图象与y轴的交点为(0,1),它的一个最高点和一个最低点的坐标分别为(x0,2),(x0![]() ,﹣2),
,﹣2),
(1)若函数f(x)的最小正周期为π,求函数f(x)的解析式;
(2)当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[
)时,f(x)图象上有且仅有一个最高点和一个最低点,且关于x的方程f(x)﹣a=0在区间[![]() ,
,![]() ]上有且仅有一解,求实数a的取值范围.
]上有且仅有一解,求实数a的取值范围.
【答案】(1)f(x)=2cos(2x![]() )(2)(﹣1,
)(2)(﹣1,![]() ]∪{﹣2}
]∪{﹣2}
【解析】
(1)由最高点纵坐标得A=2,由题意T=π,得到ω=2,从而有f(x)=2cos(2x+φ)再将(0,1)代入,求得cosφ![]() ,结合
,结合![]() φ<0的条件,得到φ
φ<0的条件,得到φ![]() ,从而确定出函数f(x)的解析式;
,从而确定出函数f(x)的解析式;
(2)根据当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,
)时,f(x)图象上有且仅有一个最高点和一个最低点,![]() x0
x0![]() x0
x0![]() ,得到T=π,求得ω=2,求得f(x)=2cos(2x
,得到T=π,求得ω=2,求得f(x)=2cos(2x![]() ),当x∈[
),当x∈[![]() ,
,![]() ]时,2x
]时,2x![]() ∈[
∈[![]() ,
,![]() ],研究函数y=2cost,t∈[
],研究函数y=2cost,t∈[![]() ,
,![]() ],得到结果.
],得到结果.
(1)由最高点纵坐标得A=2,
又T=π=2π÷ωω=2;
∴f(x)=2cos(2x+φ),
代入点(0,1)cosφ![]() ;
;
∵![]() φ<0,∴φ
φ<0,∴φ![]() ;
;
∴f(x)=2cos(2x![]() ).
).
(2)∵当x∈(x0,x0![]() )时,f(x)图象上有且仅有一个最高点和一个最低点,
)时,f(x)图象上有且仅有一个最高点和一个最低点,
∴![]() x0
x0![]() x0
x0![]() T=πω=2;
T=πω=2;
∴f(x)=2cos(2x![]() ).
).
f(x)﹣a=0f(x)=a;
当x∈[![]() ,
,![]() ]时,2x
]时,2x![]() ∈[
∈[![]() ,
,![]() ],
],
令t=2x![]() .则t∈[
.则t∈[![]() ,
,![]() ],
],
y=2cost,t∈[![]() ,
,![]() ],
],
函数y=2cost在[![]() ,π]上单调递减,y=2cost∈[﹣2,
,π]上单调递减,y=2cost∈[﹣2,![]() ];
];
函数y=2cost在[π,![]() ]上单调递增,y=2cost∈[﹣2,﹣1];
]上单调递增,y=2cost∈[﹣2,﹣1];
∴a∈(﹣1,![]() ]∪{﹣2};
]∪{﹣2};
故实数a的取值范围是:(1,![]() ]∪{﹣2}.
]∪{﹣2}.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 部分图象如图所示.
部分图象如图所示.
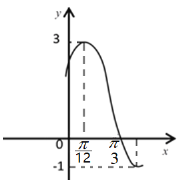
(1)求函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图象做怎样的变换可以得到函数
的图象做怎样的变换可以得到函数![]() 的图象;
的图象;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根,求
上有两个不相等的实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,当
的“类对称点”,当![]() 时,试问
时,试问![]() 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区中小学生人数和近视情况如图1和图2所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生作为样本进行调查.
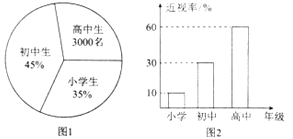
(1)求样本容量和抽取的高中生近视人数分别是多少?
(2)在抽取的![]() 名高中生中,平均每天学习时间超过9小时的人数为
名高中生中,平均每天学习时间超过9小时的人数为![]() ,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
,其中有12名学生近视,请完成高中生平均每天学习时间与近视的列联表:
平均学习时间不超过9小时 | 平均学习时间超过9小时 | 总计 | |
不近视 | |||
近视 | |||
总计 |
(3)根据(2)中的列联表,判断是否有![]() 的把握认为高中生平均每天学习时间与近视有关?
的把握认为高中生平均每天学习时间与近视有关?
附:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() ,
,![]() 的极坐标方程分别为
的极坐标方程分别为![]() ,
,![]() .
.
(1)将直线![]() 的参数方程化为极坐标方程,将
的参数方程化为极坐标方程,将![]() 的极坐标方程化为参数方程;
的极坐标方程化为参数方程;
(2)当![]() 时,直线
时,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
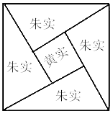
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”(如下图),四个全等的直角三角形(朱实),可以围成一个大的正方形,中空部分为一个小正方形(黄实).若直角三角形中一条较长的直角边为8,直角三角形的面积为24,若在上面扔一颗玻璃小球,则小球落在“黄实”区域的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2018年10月1日起,![]() 中华人民共和国个人所得税
中华人民共和国个人所得税![]() 新规定,公民月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
新规定,公民月工资、薪金所得不超过5000元的部分不必纳税,超过5000元的部分为全月应纳税所得额,此项税款按下表分段累计计算:
全月应纳税所得额 | 税率 |
不超过1500元的部分 | 3 |
超过1500元不超过4500元的部分 | 10 |
超过4500元不超过9000元的部分 | 20 |
超过9000元不超过35000元 | 25 |
|
|
![]() 如果小李10月份全月的工资、薪金为7000元,那么他应该纳税多少元?
如果小李10月份全月的工资、薪金为7000元,那么他应该纳税多少元?
![]() 如果小张10月份交纳税金425元,那么他10月份的工资、薪金是多少元?
如果小张10月份交纳税金425元,那么他10月份的工资、薪金是多少元?
![]() 写出工资、薪金收入
写出工资、薪金收入![]() 元
元![]() 月
月![]() 与应缴纳税金
与应缴纳税金![]() 元
元![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中,下面四个命题中不正确的是( )
翻折过程中,下面四个命题中不正确的是( )

A. ![]() 是定值
是定值
B. 点![]() 在某个球面上运动
在某个球面上运动
C. 存在某个位置,使![]()
D. 存在某个位置,使![]() 平面
平面![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com