
ЎҫМвДҝЎҝЗШҫЕЙШЛг·ЁКЗЦР№ъДПЛОКұЖЪөДКэС§јТЗШҫЕЙШМбіцөДТ»ЦЦ¶аПоКҪјт»ҜЛг·ЁЈ¬¶ФУЪЗуТ»ёцnҙО¶аПоКҪәҜКэfnЈЁxЈ©=anxn+an©Ғ1xn©Ғ1+Ўӯ+a1x+a0өДҫЯМеәҜКэЦөЈ¬ФЛУГіЈ№ж·Ҫ·ЁјЖЛгіцҪб№ыЧо¶аРиТӘnҙОјУ·ЁәН ![]() іЛ·ЁЈ¬¶шФЛУГЗШҫЕЙШЛг·ЁУЙДЪ¶шНвЦрІгјЖЛгТ»ҙО¶аПоКҪөДЦөөДЛг·ЁЦБ¶аРиТӘnҙОјУ·ЁәНnҙОіЛ·ЁЈ®¶ФУЪјЖЛг»ъАҙЛөЈ¬ЧцТ»ҙОіЛ·ЁФЛЛгЛщУГөДКұјдұИЧцТ»ҙОјУ·ЁФЛЛгТӘіӨөГ¶аЈ¬ЛщТФҙЛЛг·Ёј«ҙуөШЛх¶МБЛCPUФЛЛгКұјдЈ¬ТтҙЛјҙК№ФЪҪсМмёГЛг·ЁИФҫЯУРЦШТӘТвТеЈ®ФЛУГЗШҫЕЙШЛг·ЁјЖЛгfЈЁxЈ©=0.5x6+4x5©Ғx4+3x3©Ғ5xөұx=3КұөДЦөКұЈ¬ЧоПИјЖЛгөДКЗЈЁ Ј©
іЛ·ЁЈ¬¶шФЛУГЗШҫЕЙШЛг·ЁУЙДЪ¶шНвЦрІгјЖЛгТ»ҙО¶аПоКҪөДЦөөДЛг·ЁЦБ¶аРиТӘnҙОјУ·ЁәНnҙОіЛ·ЁЈ®¶ФУЪјЖЛг»ъАҙЛөЈ¬ЧцТ»ҙОіЛ·ЁФЛЛгЛщУГөДКұјдұИЧцТ»ҙОјУ·ЁФЛЛгТӘіӨөГ¶аЈ¬ЛщТФҙЛЛг·Ёј«ҙуөШЛх¶МБЛCPUФЛЛгКұјдЈ¬ТтҙЛјҙК№ФЪҪсМмёГЛг·ЁИФҫЯУРЦШТӘТвТеЈ®ФЛУГЗШҫЕЙШЛг·ЁјЖЛгfЈЁxЈ©=0.5x6+4x5©Ғx4+3x3©Ғ5xөұx=3КұөДЦөКұЈ¬ЧоПИјЖЛгөДКЗЈЁ Ј©
A.©Ғ5ЎБ3=©Ғ15
B.0.5ЎБ3+4=5.5
C.3ЎБ33©Ғ5ЎБ3=66
D.0.5ЎБ36+4ЎБ35=1336.6
Ўҫҙр°ёЎҝB
ЎҫҪвОцЎҝҪвЈәfЈЁxЈ©=0.5x6+4x5©Ғx4+3x3©Ғ5x=ЈЁЈЁЈЁЈЁЈЁ0.5x+4Ј©x©Ғ1Ј©x+3Ј©x+0Ј©x©Ғ5Ј©xЈ¬
И»әуУЙДЪПтНвјЖЛгЈ¬ЧоПИјЖЛгөДКЗ0.5ЎБ3+4=5.5Ј¬
№КСЎЈәBЈ®
Ўҫҝјөгҫ«ОцЎҝёщҫЭМвДҝөДТСЦӘМхјюЈ¬АыУГЗШҫЕЙШЛг·ЁөДПа№ШЦӘК¶ҝЙТФөГөҪОКМвөДҙр°ёЈ¬РиТӘХЖОХЗу¶аПоКҪөДЦөКұЈ¬КЧПИјЖЛгЧоДЪІгАЁәЕДЪТАҙО¶аПоКҪөДЦөЈ¬јҙv1=anx+an-1И»әуУЙДЪПтНвЦрІгјЖЛгТ»ҙО¶аПоКҪөДЦөЈ¬°СnҙО¶аПоКҪөДЗуЦөОКМвЧӘ»ҜіЙЗуnёцТ»ҙО¶аПоКҪөДЦөөДОКМвЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪХэ·ҪМе![]() ЦРЈ¬
ЦРЈ¬![]() ·ЦұрКЗ
·ЦұрКЗ![]() ЦРөг.
ЦРөг.

ЗуЦӨЈәЈЁ1Ј©![]() ЎОЖҪГж
ЎОЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©![]() ЖҪГж
ЖҪГж![]() .
.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬AЈ¬BЈ¬CКЗНЦФІMЈә ![]() ЙПөДИэөгЈ¬ЖдЦРөгAКЗНЦФІөДУТ¶ҘөгЈ¬BC№эНЦФІMөДЦРРДЈ¬ЗТВъЧгACЎНBCЈ¬BCЈҪ2ACЎЈ
ЙПөДИэөгЈ¬ЖдЦРөгAКЗНЦФІөДУТ¶ҘөгЈ¬BC№эНЦФІMөДЦРРДЈ¬ЗТВъЧгACЎНBCЈ¬BCЈҪ2ACЎЈ

ЈЁ1Ј©ЗуНЦФІөДАлРДВКЈ»
ЈЁ2Ј©ИфyЦбұ»ЎчABCөДНвҪУФІЛщҪШөГПТіӨОӘ9Ј¬ЗуНЦФІ·ҪіМЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР{![]() }ЦРЈ¬
}ЦРЈ¬![]() Ј¬ЗТ
Ј¬ЗТ![]() ¶ФИОТвХэХыКэ¶јіЙБўЈ¬КэБР{
¶ФИОТвХэХыКэ¶јіЙБўЈ¬КэБР{![]() }өДЗ°nПоәНОӘSnЎЈ
}өДЗ°nПоәНОӘSnЎЈ
ЈЁ1Ј©Иф![]() Ј¬ЗТ
Ј¬ЗТ![]() Ј¬ЗуaЈ»
Ј¬ЗуaЈ»
ЈЁ2Ј©КЗ·сҙжФЪКөКэkЈ¬К№КэБР{![]() }КЗ№«ұИІ»ОӘ1өДөИұИКэБРЈ¬ЗТИОТвПаБЪИэПо
}КЗ№«ұИІ»ОӘ1өДөИұИКэБРЈ¬ЗТИОТвПаБЪИэПо![]() °ҙДіЛіРтЕЕБРәуіЙөИІоКэБРЈ¬ИфҙжФЪЈ¬ЗуіцЛщУРkЦөЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
°ҙДіЛіРтЕЕБРәуіЙөИІоКэБРЈ¬ИфҙжФЪЈ¬ЗуіцЛщУРkЦөЈ¬ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
ЈЁ3Ј©Иф![]() ЎЈ
ЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЦРС§НЕОҜЧйЦҜБЛЎ°әлСп°ВФЛҫ«ЙсЈ¬°®ОТЦР»ӘЎұөДЦӘК¶ҫәИьЈ¬ҙУІОјУҝјКФөДС§ЙъЦРійіц60ГыС§ЙъЈ¬Ҫ«ЖдіЙјЁЈЁҫщОӘХыКэЈ©·ЦіЙБщ¶О[40Ј¬50Ј©Ј¬[50Ј¬60Ј©Ј¬ЎӯЈ¬[90Ј¬100Ўіәу»ӯіцИзНјЛщКҫөДЖөВК·ЦІјЦұ·ҪНјЈ®№ЫІмНјРОёшіцөДРЕПўЈ¬»ШҙрПВБРОКМвЈә 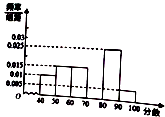
ЈЁ1Ј©ЗуөЪЛДРЎЧйөДЖөВКЈ¬ІўІ№И«ХвёцЖөВК·ЦІјЦұ·ҪНјЈ»
ЈЁ2Ј©№АјЖХвҙОҝјКФөДј°ёсВКЈЁ60·Цј°ТФЙПОӘј°ёсЈ©әНЖҪҫщ·ЦЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
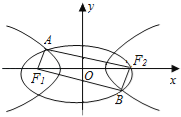
ЎҫМвДҝЎҝИзНјF1ЎўF2КЗНЦФІC1Јә![]() +y2=1УлЛ«ЗъПЯC2өД№«№ІҪ№өгЈ¬AЎўB·ЦұрКЗC1ЎўC2ФЪөЪ¶юЎўЛДПуПЮөД№«№ІөгЈ¬ИфЛДұЯРОAF1BF2ОӘҫШРОЈ¬ФтC2өДАлРДВККЗЈЁ Ј©
+y2=1УлЛ«ЗъПЯC2өД№«№ІҪ№өгЈ¬AЎўB·ЦұрКЗC1ЎўC2ФЪөЪ¶юЎўЛДПуПЮөД№«№ІөгЈ¬ИфЛДұЯРОAF1BF2ОӘҫШРОЈ¬ФтC2өДАлРДВККЗЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘөИұИКэБР{an}ВъЧгЈәa1= ![]() Ј¬a1 Ј¬ a2 Ј¬ a3©Ғ
Ј¬a1 Ј¬ a2 Ј¬ a3©Ғ ![]() іЙөИІоКэБРЈ¬№«ұИqЎКЈЁ0Ј¬1Ј©
іЙөИІоКэБРЈ¬№«ұИqЎКЈЁ0Ј¬1Ј©
ЈЁ1Ј©ЗуКэБР{an}өДНЁПКҪЈ»
ЈЁ2Ј©Йиbn=2nan Ј¬ ЗуКэБР{bn}өДЗ°nПоәНSn Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэfЈЁxЈ©=x2©Ғ2ax©Ғ2alnxЈЁaЎКRЈ©Ј¬ФтПВБРЛө·ЁХэИ·өДКЗ ўЩөұaЈј0КұЈ¬әҜКэy=fЈЁxЈ©УРБгөгЈ»
ўЪИфәҜКэy=fЈЁxЈ©УРБгөгЈ¬ФтaЈј0Ј»
ўЫҙжФЪaЈҫ0Ј¬әҜКэy=fЈЁxЈ©УРОЁТ»өДБгөгЈ»
ўЬИфәҜКэy=fЈЁxЈ©УРОЁТ»өДБгөгЈ¬ФтaЎЬ1Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() Ј®
Ј®
ЈЁўсЈ©өұ![]() КұЈ¬ЗуәҜКэ
КұЈ¬ЗуәҜКэ![]() өДј«РЎЦөЈ»
өДј«РЎЦөЈ»
ЈЁўтЈ©Йи¶ЁТеФЪ![]() ЙПөДәҜКэ
ЙПөДәҜКэ![]() ФЪөг
ФЪөг![]() ҙҰөДЗРПЯ·ҪіМОӘ
ҙҰөДЗРПЯ·ҪіМОӘ![]() Јә
Јә![]() Ј¬өұ
Ј¬өұ![]() КұЈ¬Иф
КұЈ¬Иф![]() ФЪ
ФЪ![]() ДЪәгіЙБўЈ¬ФтіЖ
ДЪәгіЙБўЈ¬ФтіЖ![]() ОӘәҜКэ
ОӘәҜКэ![]() өДЎ°ЧӘөгЎұЈ®өұ
өДЎ°ЧӘөгЎұЈ®өұ![]() КұЈ¬КФОКәҜКэ
КұЈ¬КФОКәҜКэ![]() КЗ·сҙжФЪЎ°ЧӘөгЎұЈҝИфҙжФЪЈ¬ЗуіцЧӘөгөДәбЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
КЗ·сҙжФЪЎ°ЧӘөгЎұЈҝИфҙжФЪЈ¬ЗуіцЧӘөгөДәбЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com