
| 3-1 |
| sinα | ||
1+
|
| cosα |
| 1+tanα |
| ||
| 2 |
| m |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| sinα | ||
1+
|
| cosα |
| 1+tanα |
| sin2α |
| sinα+cosα |
| cos2α |
| sinα+cosα |
| ||
| 2 |


科目:高中数学 来源: 题型:
| α |
| 2 |
| α |
| 2 |
| 1+sin2α-cos2α |
| 1+sin2α+cos2α |
| 1+sinα |
| cosα |
1+tan
| ||
1-tan
|
| 2 |
| sin2α |
查看答案和解析>>
科目:高中数学 来源: 题型:
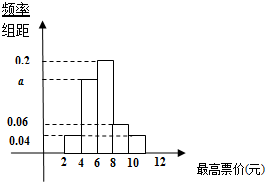 2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:
2014年5月,北京市提出地铁分段计价的相关意见,针对“你能接受的最高票价是多少?”这个问题,在某地铁站口随机对50人进行调查,调查数据的频率分布直方图及被调查者中35岁以下的人数与统计结果如下:| 最高票价 | 35岁以下人数 |
| [2,4) | 2 |
| [4,6) | 8 |
| [6,8) | 12 |
| [8,10) | 5 |
| [10,12] | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
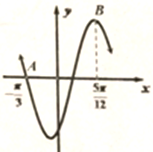 函数f(x)=2sin(ωx+φ)(ω>0,-
函数f(x)=2sin(ωx+φ)(ω>0,-| π |
| 2 |
| π |
| 2 |
A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com