
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
(1)以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,求曲线
轴的非负半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和点
的极坐标方程和点![]() 的极坐标;
的极坐标;
(2)若点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】十八届五中全会首次提出了绿色发展理念,将绿色发展作为“十三五”乃至更长时期经济社会发展的一个重要理念.某地区践行“绿水青山就是金山银山”的绿色发展理念,2015年初至2019年初,该地区绿化面积y(单位:平方公里)的数据如下表:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
绿化面积y | 2.8 | 3.5 | 4.3 | 4.7 | 5.2 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)利用(1)中的回归方程,预测该地区2025年初的绿化面积.
(参考公式:线性回归方程:![]() ,
,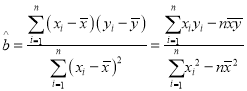 ,
,![]() 为数据平均数)
为数据平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《山东省高考改革试点方案》规定:从2017年秋季高中入学的新生开始,不分文理科;2020年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成.将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级.参照正态分布原则,确定各等级人数所占比例分别为3%、7%、16%、24%、24%、16%、7%、3%.选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71,80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩.
某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布N(60,169).
(Ⅰ)求物理原始成绩在区间(47,86)的人数;
(Ⅱ)按高考改革方案,若从全省考生中随机抽取3人,记X表示这3人中等级成绩在区间[61,80]的人数,求X的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ',
',![]() 时,
时,![]()
![]() (其中
(其中![]() 表示
表示![]() ,
,![]() ,…,
,…,![]() 中的最大项),有以下结论:
中的最大项),有以下结论:
① 若数列![]() 是常数列,则
是常数列,则![]() ;
;
② 若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
③ 若数列![]() 是公比为
是公比为![]() 的等比数列,则
的等比数列,则![]() :
:
④ 若存在正整数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则
,则![]() ,是数列
,是数列![]() 的最大项.
的最大项.
其中正确结论的序号是____(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点P(0,1)且互相垂直的两条直线分別与圆O:![]() 交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
交于点A,B,与圆M:(x﹣2)2+(y﹣1)2=1交于点C,D.
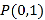
(1)若AB=![]() ,求CD的长;
,求CD的长;
(2)若CD中点为E,求△ABE面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com