Question

若满x，y足

x+2y≤4 x-y≤1 x+2≥0

，则z=3x+y的最大值为

7

．

Answer 1

分析：做出不等式组所表示的平面区域，如图所示的ABC内（包括边界），由Z=3x+y可得y=-3x+z，则z为直线y=-3x+z在y轴上的截距，作直线L：3x+y=0，则直线l向上移动到A时，Z最大，向下移动到C时，Z最小，由此规律可判断出最大值

解答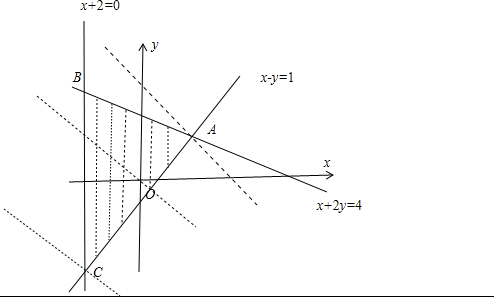：解：做出不等式组所表示的平面区域，如图所示的ABC内（包括边界）
由Z=3x+y可得y=-3x+z，则z为直线y=-3x+z在y轴上的截距
做直线L：3x+y=0，则直线l向上移动到A时，Z最大，向下移动到C时，Z最小
由

x-y=1 x+2y=4

可得A（2，1），此时Z=7
由

x-y=1 x=-2

可得C（-2，-3），此时Z=-9
故答案为7

点评：本题主要考查了利用不等式所表示的平面区域求解目标函数的最优解，解题的关键是准确做出可行域，寻求目标函数在可行域内变化的规律