
| 3 |
| 12 |
| 1 |
| 4 |
| 1 |
| 4 |
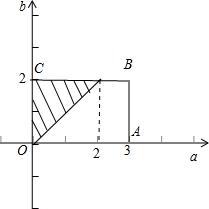
| S△OEC |
| SOABC |
| ||
| 3×2 |
| 1 |
| 3 |
| 1 |
| 3 |


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:不详 题型:解答题
| 日 期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
| 温 差 | 10 | 13 | 11 | 12 | 7 |
| 感染数 | 23 | 32 | 24 | 29 | 17 |
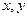 用
用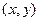 的形式列出所有的基本事件, 其中
的形式列出所有的基本事件, 其中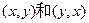 视为同一事件,并求
视为同一事件,并求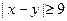 的事件A的概率。
的事件A的概率。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
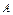 与
与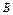 的差集
的差集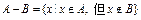 。记“从集合
。记“从集合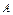 中任取一个元素
中任取一个元素 ”为事件
”为事件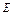 ,“从集合
,“从集合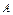 中任取一个元素
中任取一个元素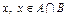 ”为事件
”为事件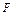 ;
;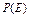 为事件
为事件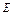 发生的概率,
发生的概率,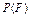 为事件
为事件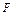 发生的概率。当
发生的概率。当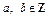 ,且
,且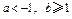 时,设集合
时,设集合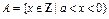 ,集合
,集合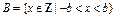 。给出下列判断: ①当
。给出下列判断: ①当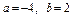 时,
时,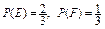 ;②总有
;②总有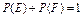 ;③若
;③若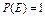 ,则
,则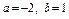 ;④
;④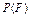 不可能等于1。其中所有判断正确的序号是 。
不可能等于1。其中所有判断正确的序号是 。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x |
| x-1 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com