
【题目】已知函数f(x)= ![]() 的图象过点A(0,
的图象过点A(0, ![]() ),B(3,3)
),B(3,3)
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性的定义加以证明;
(3)若m,n∈(2,+∞)且函数f(x)在[m,n]上的值域为[1,3],求m+n的值.
【答案】
(1)解:函数f(x)= ![]() 的图象过点A(0,
的图象过点A(0, ![]() ),B(3,3),
),B(3,3),
∴ 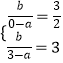 ,解得:
,解得: ![]()
∴f(x)= ![]()
(2)解:函数f(x)在(2,+∞)上单调递减,
证明:任取x2>x1>2,
则f(x1)﹣f(x2)= ![]()
∵x2>x1>2,
∴x2﹣x1>0,x1﹣2>0,x2﹣2>0,
∴ ![]() >0,得f(x1)﹣f(x2)>0,
>0,得f(x1)﹣f(x2)>0,
∴f(x1)>f(x2),
函数f(x)在(2,+∞)上是单调递减函数
(3)解:∵m,n∈(2,+∞),
∴函数f(x)在[m,n]上单调递减,
∴f(m)=3,f(n)=1
∴ ![]() =3,
=3, ![]() =1,
=1,
∴m=3,n=5,
∴m+n=8
【解析】(1)将A、B的坐标代入函数的解析式,求出a,b的值即可;(2)根据函数单调性的定义证明即可;(3)根据函数的单调性得到关于m、n的方程,求出m、n的值,从而求出m+n的值即可.
【考点精析】解答此题的关键在于理解函数单调性的判断方法的相关知识,掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


科目:高中数学 来源: 题型:
【题目】从4名男生,3名女生中选出三名代表,
(1)不同的选法共有多少种?
(2)至少有一名女生的不同的选法共有多少种?
(3)代表中男、女生都有的不同的选法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线 
(1)写出第一服药后y与t之间的函数关系式y=f(x);
(2)据进一步测定:每毫升血液中含药量不少于 ![]() 微克时,治疗有效,求服药一次后治疗有效的时间是多长?
微克时,治疗有效,求服药一次后治疗有效的时间是多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两名同学参加定点投篮测试,已知两人投中的概率分别是![]() 和
和![]() ,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
,假设两人投篮结果相互没有影响,每人各次投球是否投中也没有影响.
(Ⅰ)若每人投球3次(必须投完),投中2次或2次以上,记为达标,求甲达标的概率;
(Ⅱ)若每人有4次投球机会,如果连续两次投中,则记为达标.达标或能断定不达标,则终止投篮.记乙本次测试投球的次数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的函数f(x)= ![]() 是奇函数,其中a,b为实数
是奇函数,其中a,b为实数
(1)求a,b的值
(2)用定义证明f(x)在R上是减函数
(3)若对于任意的t∈[﹣3,3],不等式f(t2﹣2t)+f(﹣2t2+k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx,g(x)=x2 . 其中x∈R.
(1)若曲线y=f(x)与y=g(x)在x=1处的切线相互平行,求两平行直线间的距离;
(2)若f(x)≤g(x)﹣1对任意x>0恒成立,求实数a的值;
(3)当a<0时,对于函数h(x)=f(x)﹣g(x)+1,记在h(x)图象上任取两点A、B连线的斜率为kAB , 若|kAB|≥1,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com