已知圆C:(x-1)2+(y-2)2=25,直线l:(2m+1)x+(m+1)y-7m-4=0.
(1)求证:直线l恒过定点;
(2)求直线l被圆C截得的弦长的最小值及此时m的值.
(1)证明:直线l:(2m+1)x+(m+1)y-7m-4=0可化为m(2x+y-7)+(x+y-4)=0
令
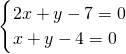
,解得

∴直线l恒过定点A(3,1)
(2)解:直线l被圆C截得的弦长的最小时,弦心距最大,此时CA⊥l
∵圆C:(x-1)
2+(y-2)
2=25,圆心(1,2),半径为5
∴CA的斜率为

=-

,
∴l的斜率为2
∵直线l:(2m+1)x+(m+1)y-7m-4=0的斜率为
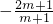
∴
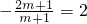
∴
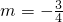
∵|CA|=

=

∴直线l被圆C截得的弦长的最小值为2
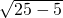
=

.
分析:(1)直线l:(2m+1)x+(m+1)y-7m-4=0可化为m(2x+y-7)+(x+y-4)=0,解方程组
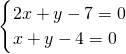
,可得直线l恒过定点;
(2)直线l被圆C截得的弦长的最小时,弦心距最大,此时CA⊥l,求出CA的斜率,可得l的斜率,从而可求m的值,求出弦心距,可得直线l被圆C截得的弦长的最小值.
点评:本题考查直线恒过定点,考查弦长的计算,解题的关键是掌握圆的特殊性,属于中档题.

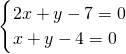 ,解得
,解得
 =-
=- ,
,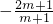
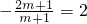
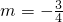
 =
=
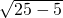 =
= .
.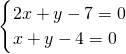 ,可得直线l恒过定点;
,可得直线l恒过定点;
