
【题目】己知函数![]() .
.
(Ⅰ)当![]() 时,解关于x的不等式
时,解关于x的不等式![]() ;
;
(Ⅱ)若不等式![]() 的解集为D,且
的解集为D,且![]() ,求m的取值范围。
,求m的取值范围。
【答案】(Ⅰ)![]() ;(II)
;(II)![]() .
.
【解析】
分析:(Ⅰ)将不等式化为一般形式,然后根据![]() 的取值情况分类讨论求解即可.(Ⅱ)将条件中的集合间的包含关系转化为不等式恒成立的问题解决,然后分离参数后再转化为求函数的最值的问题,最后根据基本不等式求解可得所求.
的取值情况分类讨论求解即可.(Ⅱ)将条件中的集合间的包含关系转化为不等式恒成立的问题解决,然后分离参数后再转化为求函数的最值的问题,最后根据基本不等式求解可得所求.
详解:(Ⅰ)由![]() 得,
得, ![]()
即![]()
①当![]() ,即
,即![]() 时,解得
时,解得![]() ;
;
②当![]() 即
即![]() 时,解得
时,解得![]() 或
或![]() ;
;
③当![]() ,即
,即![]() 时,
时,
由于 ![]() ,
,
故解得![]() .
.
综上可得:当![]() 时,解集为
时,解集为![]() 或
或![]() ;
;
当![]() 时,解集为
时,解集为![]() ;
;
当![]() 时,解集为
时,解集为![]() .
.
(II)不等式![]() 的解集为
的解集为![]() ,且
,且![]() ,即任意的
,即任意的![]() 不等式
不等式![]() 恒成立.
恒成立.
即![]() 对任意的
对任意的![]() 恒成立,
恒成立,
由于![]() ,
,
∴![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,
,
∵![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
∴![]() ,
,
∴实数![]() 的取值范围是
的取值范围是![]() .
.
另解:
不等式![]() 的解集为
的解集为![]() ,且
,且![]() ,即任意的
,即任意的![]() 不等式
不等式![]() 恒成立.设
恒成立.设![]()
(1)当![]() 时,
时,![]() ,解得
,解得![]()
(2)当![]() 时,
时,![]() , 当
, 当![]() 时恒小于0,不满足,舍去
时恒小于0,不满足,舍去
(3)当![]() 时,
时,
(ⅰ)![]() ,即
,即![]() ,得
,得![]()
(ⅱ) ,解得
,解得![]()
综上可得实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
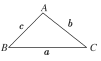
【题目】如图所示,在△ABC中,a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,在四面体PABC中,S1,S2,S3,S分别表示△PAB,△PBC,△PCA,△ABC的面积,α,β,γ依次表示面PAB,面PBC,面PCA与底面ABC所成二面角的大小.写出对四面体性质的猜想,并证明你的结论

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 中,
中, ![]() =
= ![]() =
=![]() =
= ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使
折起,使![]() .
.
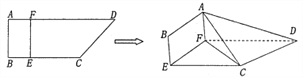
(1)若![]() ,在折叠后的线段
,在折叠后的线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(2)求三棱锥![]() 的体积的最大值,并求出此时点
的体积的最大值,并求出此时点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,函数
,函数![]() 的最小值为
的最小值为![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)求![]() ;
;
(3)已知函数![]() 为定义在上的增函数,且对任意的
为定义在上的增函数,且对任意的![]() 都满足
都满足![]() ,问:是否存在这样的实数
,问:是否存在这样的实数![]() ,使不等式
,使不等式![]() 对所有
对所有![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在边长为12的正方形AA'A1'A1中,BB1∥CC1∥AA1,且AB=3,BC=4,AA1'分别交BB1,CC1于点P,Q,将该正方形沿BB1、CC1折叠,使得A'A1'与AA1重合,构成如图2所示的三棱柱ABC﹣A1B1C1.
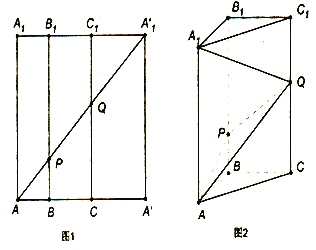
(1)求三棱锥P﹣ABC与三棱锥Q﹣PAC的体积之和;
(2)求直线AQ与平面BCC1B1所成角的正弦值;
(3)求三棱锥Q﹣ABC的外接球半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com