
【题目】孙子定理是中国古代求解一次同余式组的方法,是数论中一个重要定理,最早可见于中国南北朝时期的数学著作《孙子算经》,![]() 年英国来华传教士伟烈亚力将其问题的解法传至欧洲,
年英国来华传教士伟烈亚力将其问题的解法传至欧洲,![]() 年英国数学家马西森指出此法符合
年英国数学家马西森指出此法符合![]() 年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将
年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将![]() 至
至![]() 这
这![]() 个整数中能被
个整数中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a
(a![]() R),其中e为自然对数的底数.
R),其中e为自然对数的底数.
(1)若![]() ,求函数
,求函数![]() 的单调减区间;
的单调减区间;
(2)若函数![]() 的定义域为R,且
的定义域为R,且![]() ,求a的取值范围;
,求a的取值范围;
(3)证明:对任意![]() ,曲线
,曲线![]() 上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实现国家富强.民族复兴.人民幸福是“中国梦”的本质内涵.某商家计划以“全民健身促健康,同心共筑中国梦”为主题举办一次有奖消费活动,此商家先把某品牌乒乓球重新包装,包装时在每个乒乓球上印上“中”“国”“梦”三个字样中的一个,之后随机装盒(1盒4个球),并规定:若顾客购买的一盒球印的是同一个字,则此顾客获得一等奖;若顾客购买的一盒球集齐了“中”“国”二字且仅有此二字,则此顾客获得二等奖;若顾客购买的一盒球集齐了“中”“国”“梦”三个字,则此顾客获得三等奖,其它情况不设奖,则顾客购买一盒乒乓球获奖的概率是_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家政公司对部分员工的服务进行民意调查,调查按各项服务标准进行量化评分,婴幼儿保姆部对40~50岁和20~30岁各20名女保姆的调查结果如下:
分数 年龄 |
|
|
|
|
|
40~50岁 | 0 | 2 | 4 | 7 | 7 |
20~30岁 | 3 | 5 | 5 | 5 | 2 |
(1)若规定评分不低于80分为优秀保姆,试分别估计这两个年龄段保姆的优秀率;
(2)按照大于或等于80分为优秀保姆,80分以下为非优秀保姆统计.作出![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为对保姆工作质量的评价是否优秀与年龄有关.
的把握认为对保姆工作质量的评价是否优秀与年龄有关.
(3)从所有成绩在70分以上的人中按年龄利用分层抽样抽取10名保姆,再从这10人中选取3人给大家作经验报告,设抽到40~50岁的保姆的人数为![]() ,求出
,求出![]() 的分布列与期望值.
的分布列与期望值.
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: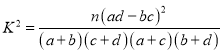 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,求
,求![]() 的面积;
的面积;
(2)若![]() ,试问椭圆
,试问椭圆![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界第一产粮大国,我国粮食产量很高,整体很安全按照14亿人口计算,中国人均粮食产量约为950斤﹣比全球人均粮食产量高了约250斤.如图是中国国家统计局网站中2010﹣2019年,我国粮食产量(千万吨)与年末总人口(千万人)的条形图,根据如图可知在2010﹣2019年中( )
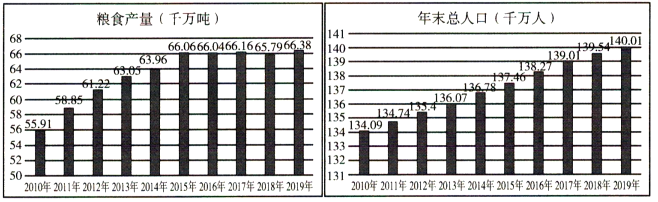
A.我国粮食年产量与年末总人口均逐年递增
B.2011年我国粮食年产量的年增长率最大
C.2015年﹣2019年我国粮食年产量相对稳定
D.2015年我国人均粮食年产量达到了最高峰
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为正项等比数列,a1=1,数列{bn}满足b2=3,a1b1+a2b2+a3b3+…+anbn=3+(2n﹣3)2n.
(1)求an;
(2)求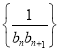 的前n项和Tn.
的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),求四边形
是坐标原点),求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com