练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某种汽车，购车费用是10万元，每年使用的保险费、养路费、汽车费约为0.9万元，年维修费第一年是0.2万元，以后逐年递增0.2万元，问这种汽车使用多少年时，它的平均费用最少？

    【答案】解：由题意知维修费用第一年是0.2万元，以后逐年递增0.2万元， 可知汽车每年维修费构成以0.2万元为首项，0.2万元为公差的等差数列，
    ∴汽车使用n年的总维修费用为0.2n+ ×0.2=0.1n（n+1）万元．
    设汽车的年平均费用为y万元，则有y=
    =1+0.1n+ ≥1+2 =3，
    当且仅当0.1n= ，即n=10时取等号，
    即当使用10年时年平均费用y最小
    【解析】汽车每年维修费构成以0.2万元为首项，0.2万元为公差的等差数列，从而表示出汽车的年平均费用，由基本不等式可得．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax﹣lnx（a∈R）．
    （1）当a=1时，求f（x）的最小值；
    （2）若存在x∈[1，3]，使 +lnx=2成立，求a的取值范围；
    （3）若对任意的x∈[1，+∞），有f（x）≥f（ ）成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在下列函数中，最小值为2的是（ ）
    A.y=2x+2﹣x
    B.y=sinx+ （0＜x＜ ）
    C.y=x+
    D.y=log3x+ （1＜x＜3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等比数列{an}满足 ，n∈N* ． （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设数列{an}的前n项和为Sn ， 若不等式Sn＞kan﹣2对一切n∈N*恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙三人投篮的水平都比较稳定，若三人各自独立地进行一次投篮测试，则甲投中而乙不投中的概率为 ，乙投中而丙不投中的概率为 ，甲、丙两人都投中的概率为 ．
    （1）分别求甲、乙、丙三人各自投篮一次投中的概率；
    （2）若丙连续投篮5次，求恰有2次投中的概率；
    （3）若丙连续投篮3次，每次投篮，投中得2分，未投中得0分，在3次投篮中，若有2次连续投中，而另外1次未投中，则额外加1分；若3次全投中，则额外加3分，记ξ为丙连续投篮3次后的总得分，求ξ的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（理科答）已知数列{an}及等差数列{bn}，若a1=3，an= an﹣1+1（n≥2），a1=b2 ， 2a3+a2=b4 ，
    （1）证明数列{an﹣2}为等比数列；
    （2）求数列{an}及数列{bn}的通项公式；
    （3）设数列{anbn}的前n项和为Tn ， 求Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，E是PC的中点，求证： （Ⅰ）PA∥平面EDB
    （Ⅱ）AD⊥PC．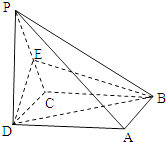

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85，乙班学生成绩的中位数是83．
    （1）求x和y的值；
    （2）计算甲班7位学生成绩的方差s2；
    （3）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平行四边形ABCD中，E，G分别是BC，DC上的点且 =3 ， =3 ，DE与BG交于点O．
    （1）求| |：| |；
    （2）若平行四边形ABCD的面积为21，求△BOC的面积．

    查看答案和解析>>

    同步练习册答案