
【题目】如图,在四棱锥![]() 中,
中,![]() ,底面四边形
,底面四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点.
上一点.

(1)若![]() ,则在线段
,则在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,请确定
?若存在,请确定![]() 点的位置;若不存在,请说明理由
点的位置;若不存在,请说明理由
(2)己知![]() ,若异面直线
,若异面直线![]() 与
与![]() 成
成![]() 角,二而角
角,二而角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的长.
的长.
【答案】(1)存在,点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点;(2)2.
的一个三等分点;(2)2.
【解析】
(1) 延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() 。通过证明
。通过证明![]() 及
及![]() ,
,![]() 可得M为PB上的一个三等分点,且靠近点P。
可得M为PB上的一个三等分点,且靠近点P。
(2)建立空间直角坐标系,写出各个点的坐标,分别求得平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,再根据二面角夹角的余弦值即可得参数t的值,进而求得CD的长。
,再根据二面角夹角的余弦值即可得参数t的值,进而求得CD的长。
解:(1)延长![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 平面
平面![]() .
.
若![]() 平面
平面![]() ,由平面
,由平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,则
,则![]() .
.
由![]() ,
,![]() ,则
,则![]() ,
,
故点![]() 是线段
是线段![]() 上靠近点
上靠近点![]() 的一个三等分点.
的一个三等分点.
(2)∵![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
则![]() 平面
平面![]()
以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴,过点
轴,过点![]() 与平面
与平面![]() 垂直的直线为
垂直的直线为![]() 轴,建立如图所示的直角坐标系,
轴,建立如图所示的直角坐标系,

则![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]()
设平面![]() 和平面
和平面![]() 的法向量分别为
的法向量分别为![]() ,
,![]() .
.
由![]() ,
,![]() 得
得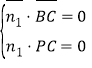 即
即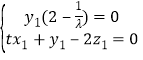 ,
,
令![]() ,则
,则![]() ,故
,故![]() .
.
同理可求得![]() .
.
于是 ,则
,则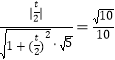 ,解之得
,解之得![]() (负值舍去),故
(负值舍去),故![]() .
.
∴![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
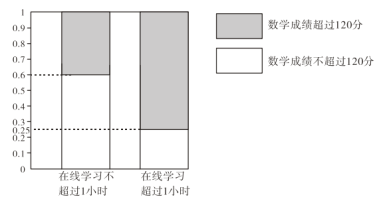
(Ⅰ)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
(Ⅱ)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
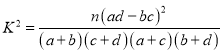
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】回文数是指从左到右读与从右到左读都一样的正整数,如11,323,4334等.在所有小于150的三位回文数中任取两个数,则两个回文数的三位数字之和均大于3的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分) 由0,1,2,3,4,5这六个数字。
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?
(3)能组成多少个无重复数字且被25个整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体对“男女延迟退休”这一公众关注的问题进行了民意调查,下表是在某单位调查后得到的数据(人数):
赞同 | 反对 | 合计 | |
男 | 5 | 6 | 11 |
女 | 11 | 3 | 14 |
合计 | 16 | 9 | 25 |
(1)能否有90%以上的把握认为对这一问题的看法与性别有关?
(2)进一步调查:
①从赞同“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行陈述发言,求事件“男士和女士各至少有
人进行陈述发言,求事件“男士和女士各至少有![]() 人发言”的概率;
人发言”的概率;
②从反对“男女延迟退休”的![]() 人中选出
人中选出![]() 人进行座谈,设选出的
人进行座谈,设选出的![]() 人中女士人数为
人中女士人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
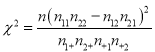
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地![]() 规划建成一个矩形的高科技工业园区.已知
规划建成一个矩形的高科技工业园区.已知![]() ,
,![]() ,
,![]() ,曲线段
,曲线段![]() 是以点
是以点![]() 为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在
为顶点且开口向上的抛物线的一段.如果要使矩形的相邻两边分别落在![]() 、
、![]() 上,且一个顶点
上,且一个顶点![]() 落在曲线段
落在曲线段![]() 上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到
上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到![]() ).
).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com