
 与
与 的夹角为120°,且满足|
的夹角为120°,且满足| |=|
|=| |=1,则|
|=1,则| +t
+t |(t∈R)的最小值是________.
|(t∈R)的最小值是________.
 +t
+t |2(t∈R)的最小值,将|
|2(t∈R)的最小值,将| +t
+t |2展开,代入题设条件,
|2展开,代入题设条件, ,
, 两向量的夹角为120°,模都是1,则可得|
两向量的夹角为120°,模都是1,则可得| +t
+t |2=t2-t+1,由于t∈R,求此二次函数的最小值即可得到|
|2=t2-t+1,由于t∈R,求此二次函数的最小值即可得到| +t
+t |2(t∈R)的最小值,再求其算术平方根,即可得到|
|2(t∈R)的最小值,再求其算术平方根,即可得到| +t
+t |的最小值,得到正确答案
|的最小值,得到正确答案 +t
+t |2(t∈R)的最小值
|2(t∈R)的最小值 +t
+t |2=
|2= +
+ +2t
+2t •
•
 ,
, 两向量的夹角为120°,模都是1
两向量的夹角为120°,模都是1 +t
+t |2=t2-t+1=
|2=t2-t+1=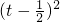 +
+ ,t∈R
,t∈R 时,|
时,| +t
+t |2取到最小值
|2取到最小值
 +t
+t |的最小值是
|的最小值是

 +t
+t |2(t∈R)的最小值,向量求模常采用的技巧就是求模的平方.本题通过二次函数求最值,用到了函数的思想,这是最值问题常用的转化方向
|2(t∈R)的最小值,向量求模常采用的技巧就是求模的平方.本题通过二次函数求最值,用到了函数的思想,这是最值问题常用的转化方向 

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:2010-2011学年山东省青岛市高三第一次模拟考试数学文卷 题型:解答题
(本小题满分12分)
设集合 ,
, ,分别从集合
,分别从集合 和
和 中随机取一个数
中随机取一个数 和
和 .
.
(Ⅰ)若向量 ,求向量
,求向量 与
与 的夹角为锐角的概率;
的夹角为锐角的概率;
(Ⅱ) 记点 ,则点
,则点 落在直线
落在直线 上为事件
上为事件
 ,
,
求使事件 的概率最大的
的概率最大的 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)设集合![]() ,
,![]() ,分别从集合
,分别从集合![]() 和
和![]() 中随机取一个数
中随机取一个数![]() 和
和![]() .
.
(Ⅰ)若向量![]() ,求向量
,求向量![]() 与
与![]() 的夹角为锐角的概率;
的夹角为锐角的概率;
(Ⅱ) 记点![]() ,则点
,则点![]() 落在直线
落在直线![]() 上为事件
上为事件![]()
![]() ,求使事件
,求使事件![]() 的概率最大的
的概率最大的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com