练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设不等式组 表示的平面区域为D，在区域D内随机取一个点，则此点到坐标原点的距离大于2的概率是 ．

    【答案】
    【解析】解：到坐标原点的距离大于2的点，位于以原点O为圆心、半径为2的圆外

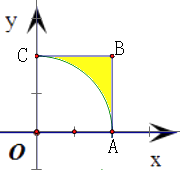
    区域D： 表示正方形OABC，（如图）

    其中O为坐标原点，A（2，0），B（2，2），C（0，2）．

    因此在区域D内随机取一个点P，

    则P点到坐标原点的距离大于2时，点P位于图中正方形OABC内，

    且在扇形OAC的外部，如图中的阴影部分

    ∵S正方形OABC=22=4，S阴影=S正方形OABC﹣S扇形OAC=4﹣ π22=4﹣π

    ∴所求概率为P= =

    所以答案是：

    【考点精析】利用几何概型对题目进行判断即可得到答案，需要熟知几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在空间四边形ABCD中，E ， F分别为AB ， AD上的点，且 ，H ， G分别为BC ， CD的中点，则( )

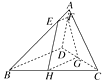
    A.BD∥平面EFGH ， 且四边形EFGH是平行四边形
    B.EF∥平面BCD ， 且四边形EFGH是梯形
    C.HG∥平面ABD ， 且四边形EFGH是平行四边形
    D.EH∥平面ADC ， 且四边形EFGH是梯形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某车间将10名技工平均分成甲、乙两组加工某种零件，在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示．已知两组技工在单位时间内加工的合格零件平均数都为9．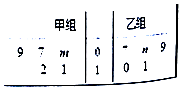

    （1）分别求出m，n的值；
    （2）分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s甲2和s乙2 ， 并由此分析两组技工的加工水平．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设y=f（x）是二次函数，方程f（x）=0有两个相等的实根，且f′（x）=2x﹣2．
    （1）求y=f（x）的表达式；
    （2）求y=f（x）的图象与两坐标轴所围成封闭图形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x（0＜x≤10）与销售价格y（单位：万元/辆）进行整理，得到如表的对应数据：

    使用年数

    2

    4

    6

    8

    10

    售价

    16

    13

    9.5

    7

    4.5


    （1）试求y关于x的回归直线方程；（参考公式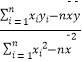： = ， =y﹣ ）
    （2）已知每辆该型号汽车的收购价格为w=0.01x3﹣0.09x2﹣1.45x+17.2万元，根据（1）中所求的回归方程，预测x为何值时，小王销售一辆该型号汽车所获得的利润L（x）最大？（利润=售价﹣收购价）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和为Sn ， 且Sn=2an﹣3n（n∈N+）．
    （1）求a1 ， a2 ， a3的值；
    （2）设bn=an+3，证明数列{bn}为等比数列，并求通项公式an ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和为Sn ， 且a1=1，an+1=2Sn+1，数列{bn}满足a1=b1 ， 点P（bn ， bn+1）在直线x﹣y+2=0上，n∈N* ．
    （1）求数列{an}，{bn}的通项公式；
    （2）设 ，求数列{cn}的前n项和Tn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数g（x）=ax2﹣2ax﹣1+b（a＞0）在区间[2，3]上有最大值4和最小值1．设f（x）= ．
    （1）求a，b的值；
    （2）若不等式f（2x）﹣k2x≥0在x∈[﹣1，1]上有解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=|ax﹣1|+|x+2|，（a＞0）．
    （Ⅰ）若a=1，时，解不等式 f（x）≤5；
    （Ⅱ）若f（x）≥2，求a的最小值．

    查看答案和解析>>

    同步练习册答案