
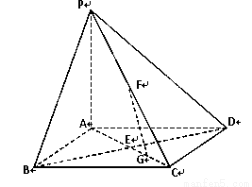
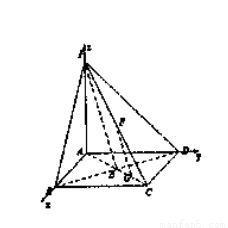
如图,在底面是正方形的四棱锥P—ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由.
(3)当二面角B—PC—D的大小为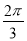 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
(1)见解析;
(2)当G为EC中点,即AG=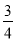 AC时,FG∥平面PBD.
AC时,FG∥平面PBD.
(3)正切值是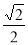 .
.
【解析】
试题分析:本题可有两种思路,一是“几何法”,二是“向量法”.
方法一:(1)先证得BD⊥平面APC ,得出BD⊥FG.
(2)注意题目中已有的中点及“等分点”,当G为EC中点,连接PE,由F为PC中点,G为EC中点,知FG∥PE, 得到FG∥平面PBD.
(3)应用“一作,二证,三计算”.
方法二:(1)以A为原点,AB,AD,PA所在的直线分别为x,y,z轴建立空间直角坐标系,
通过确定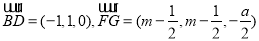 ,
,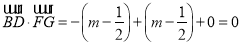
证得BD⊥FG;
(2)由 ,确定
,确定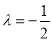 ,
,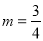 , 得到
, 得到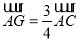 ,证得FG//平面PBD;
,证得FG//平面PBD;
(3)由 确定平面PBC的一个法向量为
确定平面PBC的一个法向量为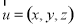 ,得到
,得到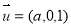 ,
,
同理可得平面PDC的一个法向量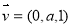 ,设
,设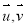 所成的角为
所成的角为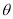 ,
,
由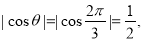
进一步确定PC与底面ABCD所成角的正切值是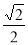 .
.
解答本题的关键是确定“垂直关系”,这也是难点所在,平时学习中,应特别注意转化意识的培养,能从“非规范几何体”,探索得到建立空间直角坐标系的条件.
方法一:(1)∵PA⊥面ABCD,四边形ABCD是正方形,其对角线BD,AC交于点E
∴PA⊥BD,AC⊥BD, ∴BD⊥平面APC 2分
∵FG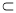 平面PAC,∴BD⊥FG 3分
平面PAC,∴BD⊥FG 3分
(2)当G为EC中点,即AG=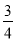 AC时,FG∥平面PBD, 4分
AC时,FG∥平面PBD, 4分
连接PE,由F为PC中点,G为EC中点,知FG∥PE, 5分
而FG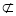 平面PBD,PB
平面PBD,PB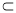 平面PBD,故FG∥平面PBD. 6分
平面PBD,故FG∥平面PBD. 6分
(3)作BH⊥PC于H,连接DH,∵PA⊥面ABCD,四边形ABCD是正方形,∴PB=PD,
又∵BC=DC,PC=PC,∴△PCB≌△PCD,∴DH⊥PC,且DH=BH,∴∠BHD是二面角B-PC-D的平面角.即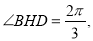 7分
7分
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角 8分
连结EH,则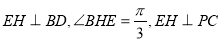 ,
,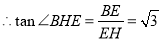
而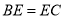 ,
,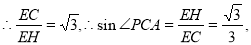 10分
10分
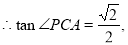 11分
11分
∴PC与底面ABCD所成角的正切值是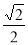 12分
12分
方法二:(1)以A为原点,AB,AD,PA所在的直线分别为x,y,z轴建立空间直角坐标系,
设正方形ABCD的边长为1,则A(0,0,0),B(1,0,0),C(1,1,0)
D(0,1,0),P(0,0,a)(a>0),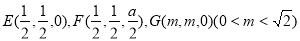 1分
1分
∵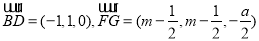 ,
,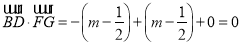 2分
2分
∴BD⊥FG 3分
(2)要使FG//平面PBD,只需FG//EP,而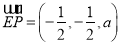 ,由
,由 ,可得:
,可得: ,解得
,解得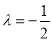 ,
,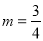 , 5分
, 5分
 ,
,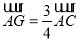 ,故当
,故当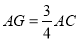 时,FG//平面PBD 6分
时,FG//平面PBD 6分
(3)设平面PBC的一个法向量为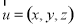
则 ,而
,而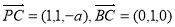
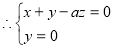 ,取
,取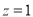 ,得
,得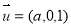 , 8分
, 8分
同理可得平面PDC的一个法向量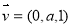 ,设
,设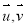 所成的角为
所成的角为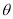 ,
,
则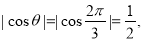
即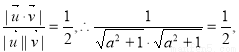
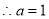 10分
10分
∵PA⊥面ABCD,∴∠PCA就是PC与底面ABCD所成的角,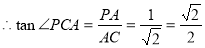
∴PC与底面ABCD所成角的正切值是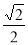 12分
12分
考点:平行关系,垂直关系,线面角的定义及计算,空间向量的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
已知双曲线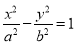 (a>0,b>0)的两条渐近线与抛物线
(a>0,b>0)的两条渐近线与抛物线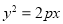 (p>0)分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
(p>0)分别交于O、A、B三点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为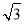 ,则p=
,则p=
A.1 B.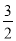 C.2 D.3
C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省德州市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
设集合M={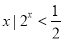 },N={
},N={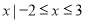 },则M
},则M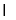 N=
N=
A.[-2,1) B.[-2,-l) C.(-1,3] D.[-2,3]
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试理科数学试卷(解析版) 题型:选择题
已知 ,函数
,函数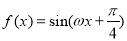 在
在 上单调递减.则
上单调递减.则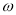 的取值范围是 ( )
的取值范围是 ( )
A.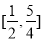 B.
B.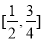 C.
C.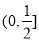 D.
D.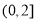
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省东营市高三4月统一质量检测考试文科数学试卷(解析版) 题型:选择题
已知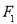 ,
,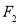 是双曲线
是双曲线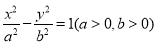 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点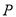 与点
与点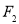 关于直线
关于直线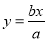 对称,则该双曲线的离心率为( )
对称,则该双曲线的离心率为( )
A.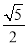 B.
B.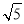 C.
C.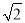 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省皖北协作区高三年级联考文科数学试卷(解析版) 题型:填空题
某公司为改善职工的出行条件,随机抽取50名职工,调查他们的居住地与公司的距离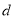 [单位:千米].若样本数据分组为
[单位:千米].若样本数据分组为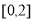 ,
, 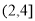 ,
,  ,
, 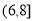 ,
, 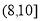 ,
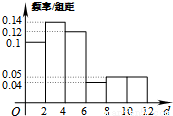
, 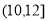 , 有数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为__________.
, 有数据绘制的频率分布直方图如图所示,则样本中职工居住地与公司的距离不超过4千米的人数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com