
【题目】已知![]() ,
,![]() .
.
(1) 求![]() 的单调区间;
的单调区间;
(2) 若![]() ,求满足
,求满足![]() 的实数
的实数![]() 的取值集合.
的取值集合.
【答案】(1) 当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
(2)![]()
【解析】(1)由![]() 可得
可得![]() ,(1分)
,(1分)
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,令
时,令![]() 可得
可得![]() ,令
,令![]() 可得
可得![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,令
时,令![]() 可得
可得![]() ,令
,令![]() 可得
可得![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(4分)
.(4分)
综上可得,当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .(5分)
.(5分)
(2)![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,
,
∴![]() 时
时![]() ,
,![]() 时
时![]() ,
,
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
∴![]() ,当且仅当
,当且仅当![]() 时取等号.(9分)
时取等号.(9分)
由(1)可知,当![]() 时,
时,![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
∴![]() 时,
时,![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
∴![]() 时,
时,![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
∴![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
即当且仅当![]() 时,
时,![]() ,
,
∴满足![]() 的实数
的实数![]() 的取值集合是
的取值集合是![]() .(12分)
.(12分)


科目:高中数学 来源: 题型:
【题目】某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准如下:85分及以上,记为A等;分数在[70,85)内,记为B等;分数在[60,70)内,记为C等;60分以下,记为D等.同时认定A,B,C为合格,D为不合格.已知某学校学生的原始成绩均分布在[50,100]内,为了了解该校学生的成绩,抽取了50名学生的原始成绩作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出样本频率分布直方图如图所示.
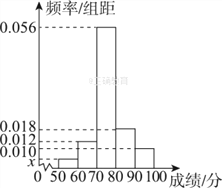
(Ⅰ)求图中x的值,并根据样本数据估计该校学生学业水平测试的合格率;
(Ⅱ)在选取的样本中,从70分以下的学生中随机抽取3名学生进行调研,用X表示所抽取的3名学生中成绩为D等级的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知由1,2,3号三位男性选手和4,5号两位女性选手组成混合组参赛.已知象棋大赛共有三轮,设三位男性选手在一至三轮胜出的概率依次是![]() ;两名女性选手在一至三轮胜出的概率依次是
;两名女性选手在一至三轮胜出的概率依次是![]() .
.
(Ⅰ)若该组五名选手与另一组选手进行小组淘汰赛,每名选手只比赛一局,共五局比赛,求该组两名女性选手的比赛次序恰好不相邻的概率;
(Ⅱ)若一位男性选手因身体不适退出比赛,剩余四人参加个人比赛,比赛结果相互不影响,设![]() 表示该组选手在四轮中胜出的人数,求随机变量
表示该组选手在四轮中胜出的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
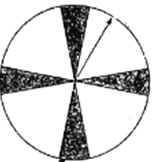
【题目】某商场举行节日促销活动,消费满一定数额即可获得一次抽奖机会,抽奖这可以从以下两种方式中任选一种进行抽奖.
抽奖方式①:让抽奖者随意转动如图所示的圆盘,圆盘停止后指针指向阴影部分(图中四个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即中奖.
,边界忽略不计)即中奖.
抽奖方式②:让抽奖者从装有3个白球和3个红球的盒子中一次性摸出2个球(球除颜色外不加区分),如果摸到的是2个红球,即中奖.
假如你是抽奖者,为了让中奖的可能性大,你应该选择哪一种抽奖方式?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在R上的奇函数,且当x≥0时, ![]() ,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
,若存在x∈[t2﹣1,t],使不等式f(2x+t)≥2f(x)成立,则实数t的取值范围是. .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,设点
,设点![]() ,且
,且![]() =2.
=2.
(1)求椭圆C的方程;
(2)已知四边形MNPQ的四个顶点均在曲线C上,且MQ∥NP,MQ⊥x轴,若直线MN和直线QP交于点S(4,0).判断四边形MNPQ两条对角线的交点是否为定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:(1)函数f(x)在[0,+∞)上是增函数,在(﹣∞,0)上也是增函数,所以f(x)在R上是增函数;(2)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0,且a>0; (3)y=x2﹣2|x|﹣3的递增区间为[1,+∞);(4)函数y=lg10x和函数y=elnx表示相同函数.其中正确命题的个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ;数列
;数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() ,
, ![]() .
.
(1)求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() 恰为数列
恰为数列![]() 中的一项?若存在,求所有满足要求的
中的一项?若存在,求所有满足要求的![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com