
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
| �Է������ | �Է������� | �ϼ� | |
| ����Ʒ���� | a=80 | b=40 | 120 |
| ����Ʒ������ | c=70 | d=10 | 80 |
| �ϼ� | 150 | 50 | n=200 |
���� ��������֪�г�������Ʒ�ͷ������۵�2��2�����������빫ʽ���k2��ֵ����Ӧ�����ô𰸣�
����ȷ�������¼��ĸ�����������ǡ��һ��Ϊ����Ʒ�������ĸ��ʣ�
��� �⣺������������ɵù�����Ʒ�ͷ������۵�2��2���������£�
| �Է������ | �Է������� | �ϼ� | |
| ����Ʒ���� | 80 | 40 | 120 |
| ����Ʒ������ | 70 | 10 | 80 |
| �ϼ� | 150 | 50 | 200 |
���� ��С����Ҫ����ͳ������ʵ����֪ʶ���Կ����Ķ����ݴ����������кܸ�Ҫ�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��1��+�ޣ� | C�� | ��0��1�� | D�� | ��1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
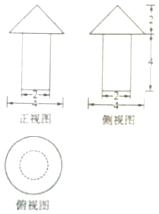
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
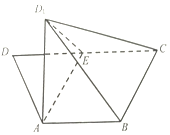 ��֪�ı���ABCD�У�AB��CD��AD=AB=BC=$\frac{1}{2}$CD=2��EΪDC�е㣬����AE������DAE��AE���۵���D1AE��
��֪�ı���ABCD�У�AB��CD��AD=AB=BC=$\frac{1}{2}$CD=2��EΪDC�е㣬����AE������DAE��AE���۵���D1AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com